Note

https://docs.doubleml.org/stable/examples/py_double_ml_apo.ipynb

Python: Average Potential Outcome (APO) Models#

In this example, we illustrate how the DoubleML package can be used to estimate average potential outcomes (APOs) in an interactive regression model (see DoubleMLIRM).

The goal is to estimate the average potential outcome

\[\theta_0 =\mathbb{E}[Y(d)]\]

for a given treatment level \(d\) and and discrete valued treatment \(D\).

[1]:

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.linear_model import LogisticRegression, LinearRegression
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor

import doubleml as dml
from doubleml.datasets import make_irm_data_discrete_treatments

Data Generating Process (DGP)#

At first, let us generate data according to the make_irm_data_discrete_treatments data generating process. The process generates data with a continuous treatment variable and contains the true individual treatment effects (ITEs) with respect to option of not getting treated.

According to the continuous treatment variable, the treatment is discretized into multiple levels, based on quantiles. Using the oracle ITEs, enables the comparison to the true APOs and averate treatment effects (ATEs) for the different levels of the treatment variable.

Remark: The average potential outcome model does not require an underlying continuous treatment variable. The model will work identically if the treatment variable is discrete by design.

[2]:

# Parameters
n_obs = 3000
n_levels = 5
linear = True
n_rep = 10

np.random.seed(42)
data_apo = make_irm_data_discrete_treatments(n_obs=n_obs,n_levels=n_levels, linear=linear)

y0 = data_apo['oracle_values']['y0']
cont_d = data_apo['oracle_values']['cont_d']
ite = data_apo['oracle_values']['ite']
d = data_apo['d']
potential_level = data_apo['oracle_values']['potential_level']
level_bounds = data_apo['oracle_values']['level_bounds']

average_ites = np.full(n_levels + 1, np.nan)
apos = np.full(n_levels + 1, np.nan)
mid_points = np.full(n_levels, np.nan)

for i in range(n_levels + 1):
    average_ites[i] = np.mean(ite[d == i]) * (i > 0)
    apos[i] = np.mean(y0) + average_ites[i]

print(f"Average Individual effects in each group:\n{np.round(average_ites,2)}\n")
print(f"Average Potential Outcomes in each group:\n{np.round(apos,2)}\n")
print(f"Levels and their counts:\n{np.unique(d, return_counts=True)}")

Average Individual effects in each group:
[ 0.    1.75  7.03  9.43 10.4  10.49]

Average Potential Outcomes in each group:
[210.04 211.79 217.06 219.47 220.44 220.53]

Levels and their counts:
(array([0., 1., 2., 3., 4., 5.]), array([615, 487, 465, 482, 480, 471]))

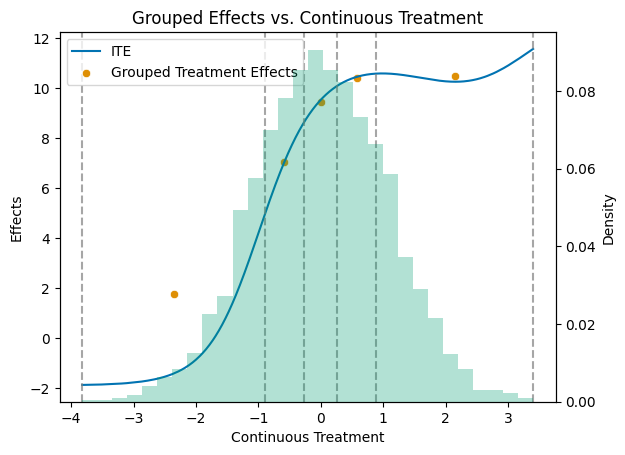
To better grasp the distribution of the treatment effects, let us plot the true APOs and ATEs.

[3]:

# Get a colorblind-friendly palette
palette = sns.color_palette("colorblind")

df = pd.DataFrame({'cont_d': cont_d, 'ite': ite})
df_sorted = df.sort_values('cont_d')

mid_points = np.full(n_levels, np.nan)
for i in range(n_levels):
    mid_points[i] = (level_bounds[i] + level_bounds[i + 1]) / 2

df_apos = pd.DataFrame({'mid_points': mid_points, 'treatment effects': apos[1:] - apos[0]})

# Create the primary plot with scatter and line plots
fig, ax1 = plt.subplots()

sns.lineplot(data=df_sorted, x='cont_d', y='ite', color=palette[0], label='ITE', ax=ax1)
sns.scatterplot(data=df_apos, x='mid_points', y='treatment effects', color=palette[1], label='Grouped Treatment Effects', ax=ax1)

# Add vertical dashed lines at level_bounds
for bound in level_bounds:
    ax1.axvline(x=bound, color='grey', linestyle='--', alpha=0.7)

ax1.set_title('Grouped Effects vs. Continuous Treatment')
ax1.set_xlabel('Continuous Treatment')
ax1.set_ylabel('Effects')

# Create a secondary y-axis for the histogram
ax2 = ax1.twinx()

# Plot the histogram on the secondary y-axis
ax2.hist(df_sorted['cont_d'], bins=30, alpha=0.3, weights=np.ones_like(df_sorted['cont_d']) / len(df_sorted['cont_d']), color=palette[2])
ax2.set_ylabel('Density')

# Make sure the legend includes all plots
lines, labels = ax1.get_legend_handles_labels()
ax1.legend(lines, labels, loc='upper left')

plt.show()

../_images/examples_py_double_ml_apo_6_0.png

As for all DoubleML models, we specify a DoubleMLData object to handle the data.

[4]:

y = data_apo['y']
x = data_apo['x']
d = data_apo['d']
df_apo = pd.DataFrame(
    np.column_stack((y, d, x)),
    columns=['y', 'd'] + ['x' + str(i) for i in range(data_apo['x'].shape[1])]
)

dml_data = dml.DoubleMLData(df_apo, 'y', 'd')
print(dml_data)

================== DoubleMLData Object ==================

------------------ Data summary      ------------------
Outcome variable: y
Treatment variable(s): ['d']
Covariates: ['x0', 'x1', 'x2', 'x3', 'x4']
Instrument variable(s): None
No. Observations: 3000

------------------ DataFrame info    ------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 3000 entries, 0 to 2999
Columns: 7 entries, y to x4
dtypes: float64(7)
memory usage: 164.2 KB

Single Average Potential Outcome Models (APO)#

Further, we have to specify machine learning algorithms. As in the DoubleMLIRM model, we have to set ml_m as a classifier and ml_g as a regressor (since the outcome is continuous). As in the DoubleMLIRM model, the classifier ml_m is used to estimate the conditional probability of receiving treatment level \(d\) given the covariates \(X\)

\[m_{0,d}(X) = \mathbb{E}[1\{D=d\}|X]\]

and the regressor ml_g is used to estimate the conditional expectation of the outcome \(Y\) given the covariates \(X\) and the treatment \(D\)

\[g_{0}(D, X) = \mathbb{E}[Y|X,D].\]

As the DGP is linear we will use a linear regression model for the regressor and a logistic regression model for the classifier.

[5]:

ml_g = LinearRegression()
ml_m = LogisticRegression()

Further, the DoubleMLAPO model requires a specification of the treatment level \(a\) for which the APOs should be estimated. In this example, we will loop over all treatment levels.

[6]:

np.random.seed(42)

treatment_levels = np.unique(d)
thetas = np.full(n_levels + 1, np.nan)
ci = np.full((n_levels + 1, 2), np.nan)

for i_level, treatment_level in enumerate(treatment_levels):
    dml_obj = dml.DoubleMLAPO(
        dml_data,
        ml_g,
        ml_m,
        treatment_level=treatment_level,
        n_rep=n_rep,
    )

    dml_obj.fit()

    thetas[i_level] = dml_obj.coef[0]
    ci[i_level, :] = dml_obj.confint(level=0.95).values

# combine results
df_apo_ci = pd.DataFrame(
    {'treatment_level': treatment_levels,
     'apo': apos,
     'theta': thetas,
     'ci_lower': ci[:, 0],
     'ci_upper': ci[:, 1]}
)

df_apo_ci

[6]:

	treatment_level	apo	theta	ci_lower	ci_upper
0	0.0	210.036240	210.077702	208.768798	211.386831
1	1.0	211.785815	211.881937	210.545492	213.218383
2	2.0	217.063017	217.069443	215.750701	218.388185
3	3.0	219.468907	219.404300	218.096418	220.712095
4	4.0	220.439699	220.503700	219.186589	221.820963
5	5.0	220.525064	220.417834	219.095104	221.740505

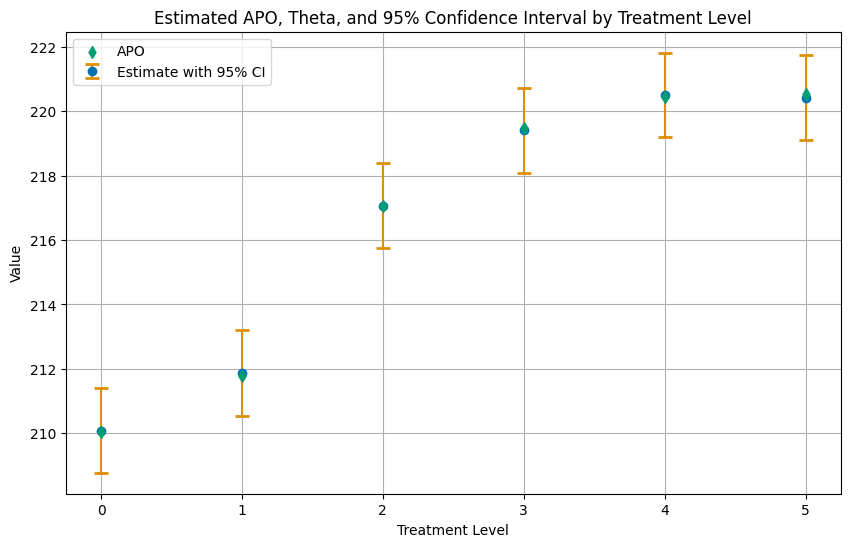
The tables above displays the estimated values in the theta column and the corresponding oracle values in the apo column.

Again, let us summarize the results in a plot of the APOs with confidence intervals.

[7]:

# Plotting
plt.figure(figsize=(10, 6))
# Plot Estimate with 95% CI
plt.errorbar(df_apo_ci['treatment_level'], df_apo_ci['theta'],
             yerr=[df_apo_ci['theta'] - df_apo_ci['ci_lower'], df_apo_ci['ci_upper'] - df_apo_ci['theta']],
             fmt='o', capsize=5, capthick=2, ecolor=palette[1], color=palette[0], label='Estimate with 95% CI', zorder=2)
# Plot APO as a scatter plot, with zorder set to 2 to be in front
plt.scatter(df_apo_ci['treatment_level'], df_apo_ci['apo'], color=palette[2], label='APO', marker='d', zorder=3)

plt.title('Estimated APO, Theta, and 95% Confidence Interval by Treatment Level')
plt.xlabel('Treatment Level')
plt.ylabel('Value')
plt.xticks(df_apo_ci['treatment_level'])
plt.legend()
plt.grid(True)
plt.show()

../_images/examples_py_double_ml_apo_14_0.png

Multiple Average Potential Outcome Models (APOS)#

Instead of looping over different treatment levels, one can directly use the DoubleMLAPOS model which internally combines multiple DoubleMLAPO models. An advantage of this approach is that the model can be parallelized, create joint confidence intervals and allow for a comparison between the average potential outcome levels.

Average Potential Outcome (APOs)#

As before, we just have to specify the machine learning algorithms and the treatment levels for which the APOs should be estimated.

[8]:

dml_obj = dml.DoubleMLAPOS(
    dml_data,
    ml_g,
    ml_m,
    treatment_levels=treatment_levels,
    n_rep=n_rep,
)

dml_obj.fit()

ci_pointwise = dml_obj.confint(level=0.95)

df_apos_ci = pd.DataFrame(
    {'treatment_level': treatment_levels,
     'apo': apos,
     'theta': thetas,
     'ci_lower': ci_pointwise.values[:, 0],
     'ci_upper': ci_pointwise.values[:, 1]}
)

df_apos_ci

[8]:

	treatment_level	apo	theta	ci_lower	ci_upper
0	0.0	210.036240	210.077702	208.766940	211.384677
1	1.0	211.785815	211.881937	210.553004	213.225427
2	2.0	217.063017	217.069443	215.756200	218.393654
3	3.0	219.468907	219.404300	218.108259	220.723846
4	4.0	220.439699	220.503700	219.192952	221.828157
5	5.0	220.525064	220.417834	219.095785	221.741523

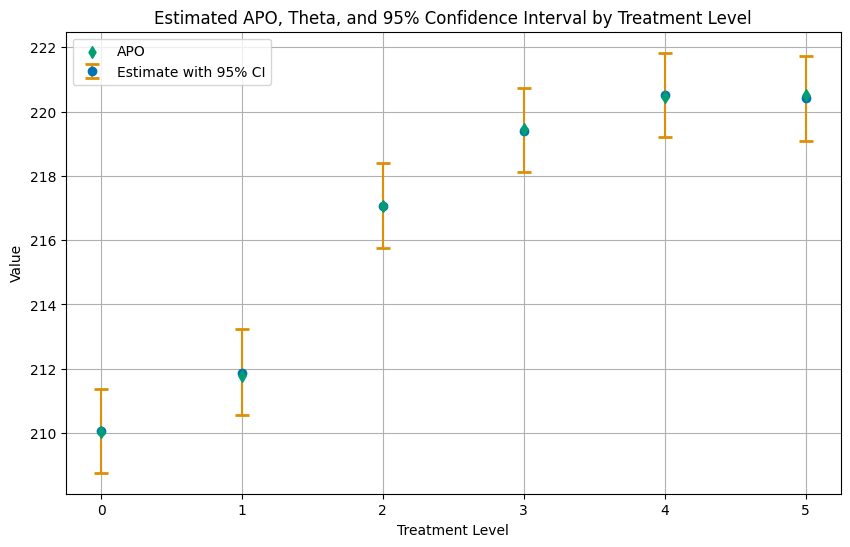
Again, let us summarize the results in a plot.

[9]:

# Plotting
plt.figure(figsize=(10, 6))
# Plot Estimate with 95% CI
plt.errorbar(df_apos_ci['treatment_level'], df_apos_ci['theta'],
             yerr=[df_apos_ci['theta'] - df_apos_ci['ci_lower'], df_apos_ci['ci_upper'] - df_apos_ci['theta']],
             fmt='o', capsize=5, capthick=2, ecolor=palette[1], color=palette[0], label='Estimate with 95% CI', zorder=2)
# Plot APO as a scatter plot, with zorder set to 2 to be in front
plt.scatter(df_apos_ci['treatment_level'], df_apos_ci['apo'], color=palette[2], label='APO', marker='d', zorder=3)

plt.title('Estimated APO, Theta, and 95% Confidence Interval by Treatment Level')
plt.xlabel('Treatment Level')
plt.ylabel('Value')
plt.xticks(df_apos_ci['treatment_level'])
plt.legend()
plt.grid(True)
plt.show()

../_images/examples_py_double_ml_apo_18_0.png

For joint confidence intervals, the bootstrap method can be used.

[10]:

dml_obj.bootstrap(n_rep_boot=2000)
ci_joint = dml_obj.confint(level=0.95, joint=True)

ci_joint

[10]:

	2.5 %	97.5 %
0.0	208.642329	211.518478
1.0	210.419871	213.355065
2.0	215.622272	218.521233
3.0	217.975289	220.850038
4.0	219.058375	221.962364
5.0	218.968127	221.878746

Sensitivity Analysis#

For DoubleMLAPO and DoubleMLAPOS model all methods for sensitivity analysis are available.

[11]:

dml_obj.sensitivity_analysis()
print(dml_obj.sensitivity_summary)

================== Sensitivity Analysis ==================

------------------ Scenario          ------------------
Significance Level: level=0.95
Sensitivity parameters: cf_y=0.03; cf_d=0.03, rho=1.0

------------------ Bounds with CI    ------------------
     CI lower  theta lower       theta  theta upper    CI upper
0  208.728734   209.827445  210.075809   210.324476  211.422561
1  210.397179   211.516945  211.889638   212.261520  213.385013
2  215.581896   216.687697  217.074927   217.461646  218.569444
3  217.966320   219.064175  219.416052   219.767616  220.865074
4  219.057274   220.163816  220.510555   220.857294  221.962523
5  218.890229   220.003111  220.418741   220.832078  221.940450

------------------ Robustness Values ------------------
   H_0     RV (%)    RVa (%)
0  0.0  99.849245  99.835822
1  0.0  99.670785  99.622750
2  0.0  99.659361  99.625183
3  0.0  99.725080  99.699543
4  0.0  99.734278  99.708821
5  0.0  99.621902  99.577647

Additionally, sensitvity_benchmark can be used. In this example we benchmark covariate x4 which does not affect treatment \(D\) or outcome \(Y\).

[12]:

dml_obj.sensitivity_benchmark(benchmarking_set=['x4'])

[12]:

	cf_d	rho	delta_theta
0.0	0.000000	0.0	0.000006
1.0	0.000000	-1.0	-0.004253
2.0	0.000000	1.0	0.003220
3.0	0.000000	-1.0	-0.004526
4.0	0.003415	1.0	0.003404
5.0	0.000000	-1.0	-0.006055

For more details on the sensitivity analysis, please refer to the User Guide.

Causal Contrasts#

The DoubleMLAPOS model also allows for the estimation of causal contrasts. The contrast is defined as the difference in the average potential outcomes between the treatment levels \(d_i\) and \(d_j\) where

\[\theta_{0,ij} = \mathbb{E}[Y(d_i)] - \mathbb{E}[Y(d_{j})]\]

and will be calculated for all defined treatment levels \(i\) and reference levels \(j\).

In this example, we will estimate the causal contrast between the treatment level \(0\) and all other treatment levels, as the treatment level \(0\) corresponds to no treatment at all whereas the the other levels are based on the treatment dosage.

Therefore we have to specify reference_levels=0.

[13]:

causal_contrast_model = dml_obj.causal_contrast(reference_levels=0)
print(causal_contrast_model.summary)

                 coef   std err          t  P>|t|      2.5 %     97.5 %
1.0 vs 0.0   1.810306  0.180143  10.049264    0.0   1.454406   2.165707
2.0 vs 0.0   6.994208  0.145027  48.226969    0.0   6.710059   7.278035
3.0 vs 0.0   9.335446  0.135344  68.975592    0.0   9.068934   9.600776
4.0 vs 0.0  10.431998  0.141460  73.745022    0.0  10.155160  10.708837
5.0 vs 0.0  10.342362  0.155174  66.650234    0.0  10.039141  10.645583

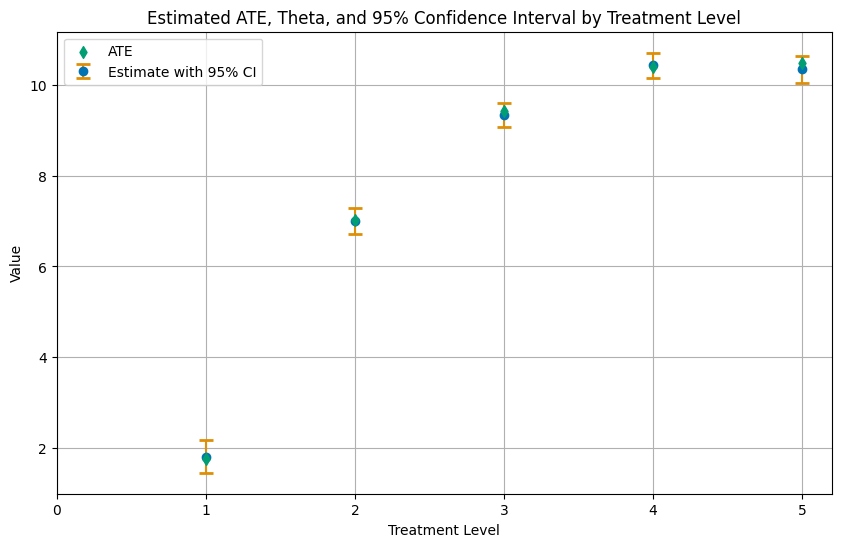
Finally, let us summarize the results in a plot.

[14]:

ates = causal_contrast_model.thetas
ci_ates = causal_contrast_model.confint(level=0.95)

df_ates = pd.DataFrame(
    {'treatment_level': treatment_levels[1:],
     'ate': ates,
     'ci_lower': ci_ates.iloc[:, 0].values,
     'ci_upper': ci_ates.iloc[:, 1].values}
)

# Plotting
plt.figure(figsize=(10, 6))
# Plot Estimate with 95% CI
plt.errorbar(df_ates['treatment_level'], df_ates['ate'],
             yerr=[df_ates['ate'] - df_ates['ci_lower'], df_ates['ci_upper'] - df_ates['ate']],
             fmt='o', capsize=5, capthick=2, ecolor=palette[1], color=palette[0], label='Estimate with 95% CI', zorder=2)
# Plot APO as a scatter plot, with zorder set to 2 to be in front
plt.scatter(df_apos_ci['treatment_level'][1:], average_ites[1:], color=palette[2], label='ATE', marker='d', zorder=3)

plt.title('Estimated ATE, Theta, and 95% Confidence Interval by Treatment Level')
plt.xlabel('Treatment Level')
plt.ylabel('Value')
plt.xticks(df_apos_ci['treatment_level'])
plt.legend()
plt.grid(True)
plt.show()

../_images/examples_py_double_ml_apo_29_0.png

The methods sensitivity_analysis and sensitivity_plot are also available for the causal contrasts.

[15]:

causal_contrast_model.sensitivity_analysis()
print(causal_contrast_model.sensitivity_summary)

================== Sensitivity Analysis ==================

------------------ Scenario          ------------------
Significance Level: level=0.95
Sensitivity parameters: cf_y=0.03; cf_d=0.03, rho=1.0

------------------ Bounds with CI    ------------------
            CI lower  theta lower      theta  theta upper   CI upper
1.0 vs 0.0  0.978997     1.278522   1.810306     2.344753   2.640334
2.0 vs 0.0  6.200065     6.441676   6.994208     7.546266   7.782117
3.0 vs 0.0  8.599208     8.825801   9.335446     9.842589  10.063685
4.0 vs 0.0  9.698651     9.934068  10.431998    10.933259  11.163577
5.0 vs 0.0  9.536219     9.797157  10.342362    10.887197  11.138953

------------------ Robustness Values ------------------
            H_0     RV (%)    RVa (%)
1.0 vs 0.0  0.0   9.818313   8.218176
2.0 vs 0.0  0.0  31.816645  30.614201
3.0 vs 0.0  0.0  42.377195  41.204626
4.0 vs 0.0  0.0  46.536082  45.315223
5.0 vs 0.0  0.0  43.385615  41.944839

As an example see the sensitivity_plot for the first causal contrast 1.0 vs 0.0.

[16]:

causal_contrast_model.sensitivity_plot(idx_treatment=0)

Benchmarking is not available for causal contrasts.