Note
-
Download Jupyter notebook:
https://docs.doubleml.org/stable/examples/R_double_ml_did.ipynb.
R: DoubleML for Difference-in-Differences#
In this example, we demonstrate, how DoubleML can be used in combination with the did package for R in order to estimate group-time average treatment effects in difference-in-difference (DiD) models with multiple periods.
[1]:
library(DoubleML)
library(did)
library(mlr3)
library(mlr3learners)
# suppress messages during fitting
lgr::get_logger("mlr3")$set_threshold("warn")
set.seed(1234)
Demo Example from did#
We will demonstrate the use of DoubleML for DiD in the introductory example of the did package.
[2]:
# Generate data, original code available at https://github.com/bcallaway11/did/blob/master/vignettes/did-basics.Rmd
time.periods <- 4
sp <- reset.sim()
sp$te <- 0
set.seed(1814)
# generate dataset with 4 time periods
time.periods <- 4
# add dynamic effects
sp$te.e <- 1:time.periods
# generate data set with these parameters
# here, we dropped all units who are treated in time period 1 as they do not help us recover ATT(g,t)'s.
dta <- build_sim_dataset(sp)
# How many observations remained after dropping the ``always-treated'' units
nrow(dta)
#This is what the data looks like
head(dta)
| G | X | id | cluster | period | Y | treat |
|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <int> | <int> | <dbl> | <dbl> | <dbl> |
| 3 | -0.8762330 | 1 | 5 | 1 | 5.562556 | 1 |
| 3 | -0.8762330 | 1 | 5 | 2 | 4.349213 | 1 |
| 3 | -0.8762330 | 1 | 5 | 3 | 7.134037 | 1 |
| 3 | -0.8762330 | 1 | 5 | 4 | 6.243056 | 1 |
| 2 | -0.8738481 | 2 | 36 | 1 | -3.659387 | 1 |
| 2 | -0.8738481 | 2 | 36 | 2 | -1.274099 | 1 |
Comparison to did package#
By default, estimation in did is based on (unpenalized) linear and logistic regression. Let’s start with this default model first.
[3]:
# estimate group-time average treatment effects using att_gt method
example_attgt <- att_gt(yname = "Y",
tname = "period",
idname = "id",
gname = "G",
xformla = ~X,
data = dta
)
# summarize the results
summary(example_attgt)
Call:
att_gt(yname = "Y", tname = "period", idname = "id", gname = "G",
xformla = ~X, data = dta)
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
Group-Time Average Treatment Effects:
Group Time ATT(g,t) Std. Error [95% Simult. Conf. Band]
2 2 0.9209 0.0638 0.7486 1.0932 *
2 3 1.9875 0.0633 1.8164 2.1586 *
2 4 2.9552 0.0680 2.7715 3.1389 *
3 2 -0.0433 0.0660 -0.2215 0.1349
3 3 1.1080 0.0670 0.9271 1.2890 *
3 4 2.0590 0.0652 1.8828 2.2352 *
4 2 0.0023 0.0634 -0.1690 0.1736
4 3 0.0615 0.0643 -0.1122 0.2353
4 4 0.9523 0.0691 0.7656 1.1391 *
---
Signif. codes: `*' confidence band does not cover 0
P-value for pre-test of parallel trends assumption: 0.60857
Control Group: Never Treated, Anticipation Periods: 0
Estimation Method: Doubly Robust
Using ML for DiD: Integrating DoubleML in did#
As described in our Section on DiD models in the user guide, Sant’Anna and Zhao (2020) have developed a doubly robust DiD model which is compatible with ML-based estimation. As this doubly robust model is internally used in did, it is possible to use DoubleML here to obtain valid point estimates and confidence intervals. For
this, we need to write a wrapper around a DoubleMLIRM model and pass it to did as a custom estimation approach. Once this is implemented, we can use all the nice features and advantages of the did package.
For now, let’s abstract from using fancy ML algorithms to keep the comparison to the classic did implementation simple. Hence, we will use linear and logistic regression for the nuisance compontents in the DiD model.
[4]:
# DoubleML wrapper for did
set.seed(1234)
doubleml_did_linear <- function(y1, y0, D, covariates,
ml_g = lrn("regr.lm"),
ml_m = lrn("classif.log_reg"),
n_folds = 10, n_rep = 1, ...) {
# warning if n_rep > 1 to handle mapping from psi to inf.func
if (n_rep > 1) {
warning("n_rep > 1 is not supported.")
}
# Compute difference in outcomes
delta_y <- y1 - y0
# Prepare data backend
dml_data = DoubleML::double_ml_data_from_matrix(X = covariates, y = delta_y, d = D)
# Compute the ATT
dml_obj = DoubleML::DoubleMLIRM$new(dml_data, ml_g = ml_g, ml_m = ml_m, score = "ATTE", n_folds = n_folds)
dml_obj$fit()
att = dml_obj$coef[1]
# Return results
inf.func <- dml_obj$psi[, 1, 1]
output <- list(ATT = att, att.inf.func = inf.func)
return(output)
}
example_attgt_dml_linear <- att_gt(yname = "Y",
tname = "period",
idname = "id",
gname = "G",
xformla = ~X,
data = dta,
est_method = doubleml_did_linear)
summary(example_attgt_dml_linear)
Call:
att_gt(yname = "Y", tname = "period", idname = "id", gname = "G",
xformla = ~X, data = dta, est_method = doubleml_did_linear)
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
Group-Time Average Treatment Effects:
Group Time ATT(g,t) Std. Error [95% Simult. Conf. Band]
2 2 0.9145 0.0646 0.7368 1.0922 *
2 3 1.9951 0.0631 1.8215 2.1687 *
2 4 2.9561 0.0622 2.7850 3.1273 *
3 2 -0.0418 0.0629 -0.2147 0.1312
3 3 1.1041 0.0651 0.9251 1.2830 *
3 4 2.0533 0.0658 1.8725 2.2341 *
4 2 -0.0028 0.0718 -0.2002 0.1946
4 3 0.0635 0.0663 -0.1188 0.2458
4 4 0.9609 0.0690 0.7711 1.1507 *
---
Signif. codes: `*' confidence band does not cover 0
P-value for pre-test of parallel trends assumption: 0.64579
Control Group: Never Treated, Anticipation Periods: 0
Any differences from the default did implementation arise due to sampling randomness, because DoubleML uses cross-fitting internally, which is not necessary if classical parametric estimation methods are used.
Next, let’s demonstrate how we can use more complex ML learners. For this, we just have to pass another mlr3 learner through the wrapper, for example a random forest. Please note that the original data generating process is linear, such that we don’t expect random forest to lead to better results than the linear learners. We provide a variant of the wrapper that includes an evaluation of the nuisance predictions at the end of this notebook.
[5]:
# DoubleML wrapper for did with random forest learner
set.seed(1234)
doubleml_did_rf <- function(y1, y0, D, covariates,
ml_g = lrn("regr.ranger"),
ml_m = lrn("classif.ranger"),
n_folds = 10, n_rep = 1, ...) {
# warning if n_rep > 1 to handle mapping from psi to inf.func
if (n_rep > 1) {
warning("n_rep > 1 is not supported.")
}
# Compute difference in outcomes
delta_y <- y1 - y0
# Prepare data backend
dml_data = DoubleML::double_ml_data_from_matrix(X = covariates, y = delta_y, d = D)
# Compute the ATT
dml_obj = DoubleML::DoubleMLIRM$new(dml_data, ml_g = ml_g, ml_m = ml_m, score = "ATTE", n_folds = n_folds)
dml_obj$fit()
att = dml_obj$coef[1]
# Return results
inf.func <- dml_obj$psi[, 1, 1]
output <- list(ATT = att, att.inf.func = inf.func)
return(output)
}
example_attgt_dml_rf <- att_gt(yname = "Y",
tname = "period",
idname = "id",
gname = "G",
xformla = ~X,
data = dta,
est_method = doubleml_did_rf)
summary(example_attgt_dml_rf)
Call:
att_gt(yname = "Y", tname = "period", idname = "id", gname = "G",
xformla = ~X, data = dta, est_method = doubleml_did_rf)
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
Group-Time Average Treatment Effects:
Group Time ATT(g,t) Std. Error [95% Simult. Conf. Band]
2 2 0.9647 0.0698 0.7733 1.1562 *
2 3 2.1055 0.0879 1.8643 2.3467 *
2 4 3.1295 0.1056 2.8397 3.4192 *
3 2 0.0820 0.0702 -0.1106 0.2747
3 3 1.2075 0.0704 1.0144 1.4006 *
3 4 2.2865 0.0889 2.0428 2.5302 *
4 2 0.1807 0.0713 -0.0149 0.3763
4 3 0.2451 0.0675 0.0599 0.4302 *
4 4 1.1401 0.0698 0.9485 1.3316 *
---
Signif. codes: `*' confidence band does not cover 0
P-value for pre-test of parallel trends assumption: 2e-05
Control Group: Never Treated, Anticipation Periods: 0
We can see that the results are not dramatically different from the results before. We can observe from the larger standard errors that the default random forest learners seems to be a less precise prediction rule.
Exploiting the Functionalities of did#
The did package offers various tools for multi-period DiD models, for example plotting the group-time average treatment effects, which can be exploited just as in the native did usage.
[6]:
# Plot group-time average treatment effects
ggdid(example_attgt_dml_linear)
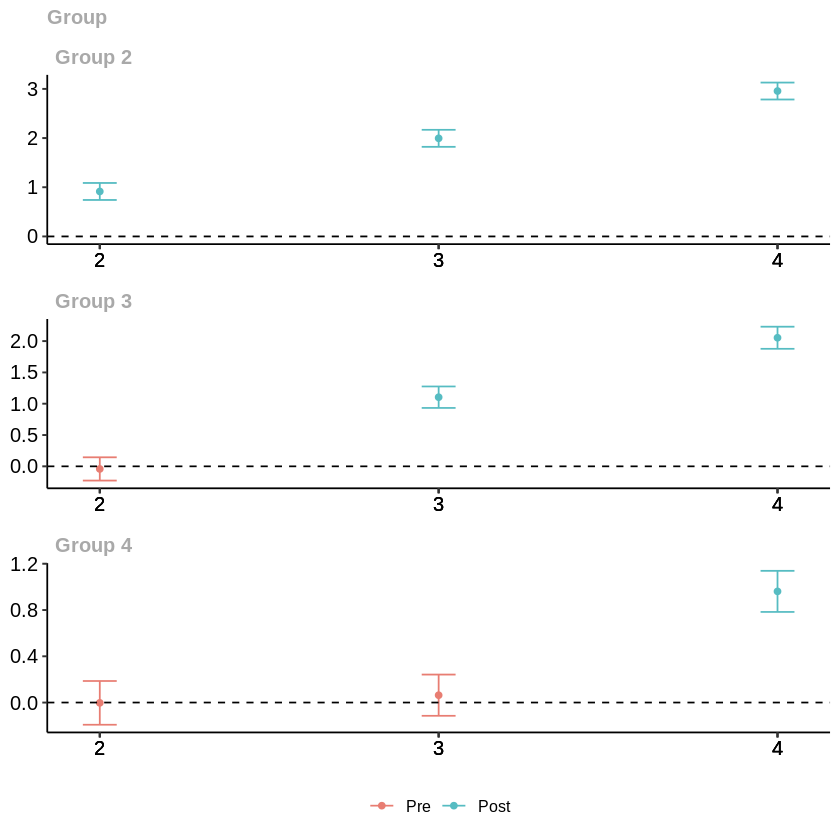
It’s also possible to calculate aggregated effect estimates. Please note that, the results are again very close to those in the original notebook.
[7]:
agg.simple <- aggte(example_attgt_dml_linear, type = "simple")
summary(agg.simple)
Call:
aggte(MP = example_attgt_dml_linear, type = "simple")
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
ATT Std. Error [ 95% Conf. Int.]
1.6586 0.0363 1.5875 1.7297 *
---
Signif. codes: `*' confidence band does not cover 0
Control Group: Never Treated, Anticipation Periods: 0
Details on Predictive Performance#
We can add an evaluation functionality to the wrapper to assess how the predictive performance from the linear and logistic regression differ from that of the random forest learner.
[8]:
library(mlr3measures)
# Add a wrapper that computes the RMSE and accuracy for the nuisance components, can be customized by providing custom measures
eval_preds = function(y, d, predictions, params_names, custom_measures = NULL) {
measures_res = list()
if (!is.null(custom_measures)) {
# Alternatively provide a named list with custom evaluation functions
measure_funcs = list()
} else {
measure_funcs = list()
measure_funcs[['ml_m']] = mlr3measures::acc
measure_funcs[['ml_g0']] = mlr3measures::rmse
}
for (param_name in params_names) {
preds = predictions[[param_name]][, 1, 1]
if (param_name == "ml_m") {
obs = d
# map probability predictions to binary
preds = as.factor(ifelse(preds > 0.5, 1, 0))
obs = as.factor(preds)
}
else if (param_name == "ml_g0") {
obs = y[d == 0]
preds = preds[d == 0]
}
if (param_name == "ml_g1") {
next
}
else {
measure_func = measure_funcs[[param_name]]
measure_pred = measure_func(obs, preds)
measures_res[[param_name]] = measure_pred
}
}
return(measures_res)
}
# evaluate learner performance: linear models
doubleml_did_eval_linear <- function(y1, y0, D, covariates,
ml_g = lrn("regr.lm"),
ml_m = lrn("classif.log_reg"),
n_folds = 10, n_rep = 1, ...) {
# warning if n_rep > 1 to handle mapping from psi to inf.func
if (n_rep > 1) {
warning("n_rep > 1 is not supported.")
}
# Compute difference in outcomes
delta_y <- y1 - y0
# Prepare data backend
dml_data = DoubleML::double_ml_data_from_matrix(X = covariates, y = delta_y, d = D)
# Compute the ATT
dml_obj = DoubleML::DoubleMLIRM$new(dml_data, ml_g = ml_g, ml_m = ml_m, score = "ATTE", n_folds = n_folds)
dml_obj$fit(store_predictions = TRUE)
att = dml_obj$coef[1]
# Return results
inf.func <- dml_obj$psi[, 1, 1]
# Evaluate learner performance
predictions = dml_obj$predictions
params_names = dml_obj$params_names()
eval_predictions = eval_preds(delta_y, D, predictions, params_names)
print(eval_predictions)
output <- list(ATT = att, att.inf.func = inf.func)
return(output)
}
library(mlr3measures)
# evaluate learner performance: random forest
doubleml_did_eval_rf <- function(y1, y0, D, covariates,
ml_g = lrn("regr.ranger"),
ml_m = lrn("classif.ranger"),
n_folds = 10, n_rep = 1, ...) {
# warning if n_rep > 1 to handle mapping from psi to inf.func
if (n_rep > 1) {
warning("n_rep > 1 is not supported.")
}
# Compute difference in outcomes
delta_y <- y1 - y0
# Prepare data backend
dml_data = DoubleML::double_ml_data_from_matrix(X = covariates, y = delta_y, d = D)
# Compute the ATT
dml_obj = DoubleML::DoubleMLIRM$new(dml_data, ml_g = ml_g, ml_m = ml_m, score = "ATTE", n_folds = n_folds)
dml_obj$fit(store_predictions = TRUE)
att = dml_obj$coef[1]
# Return results
inf.func <- dml_obj$psi[, 1, 1]
# Evaluate learner performance
predictions = dml_obj$predictions
params_names = dml_obj$params_names()
eval_predictions = eval_preds(delta_y, D, predictions, params_names)
print(eval_predictions)
output <- list(ATT = att, att.inf.func = inf.func)
return(output)
}
In order to avoid name clashes, do not attach 'mlr3measures'. Instead, only load the namespace with `requireNamespace("mlrmeasures")` and access the measures directly via `::`, e.g. `mlr3measures::auc()`.
Running the evaluation wrappers helps to see that the random forest learner has a higher RMSE for predicting the outcome \(E[\Delta Y|D=1,X]\). Both models predict individuals’ treatment (group) status with an accuracy of \(1\).
[9]:
# Run estimation with evaluation: Linear model
set.seed(1234)
example_attgt_dml_eval_linear <- att_gt(yname = "Y",
tname = "period",
idname = "id",
gname = "G",
xformla = ~X,
data = dta,
est_method = doubleml_did_eval_linear,
print_details = TRUE)
summary(example_attgt_dml_eval_linear)
Evaluating (g,t) = (2,1)$ml_g0
[1] 1.425103
$ml_m
[1] 1
Evaluating (g,t) = (2,2)$ml_g0
[1] 1.409154
$ml_m
[1] 1
Evaluating (g,t) = (2,3)$ml_g0
[1] 1.397313
$ml_m
[1] 1
Evaluating (g,t) = (3,1)$ml_g0
[1] 1.425493
$ml_m
[1] 1
Evaluating (g,t) = (3,2)$ml_g0
[1] 1.40676
$ml_m
[1] 1
Evaluating (g,t) = (3,3)$ml_g0
[1] 1.421083
$ml_m
[1] 1
Evaluating (g,t) = (4,1)$ml_g0
[1] 1.426055
$ml_m
[1] 1
Evaluating (g,t) = (4,2)$ml_g0
[1] 1.40583
$ml_m
[1] 1
Evaluating (g,t) = (4,3)$ml_g0
[1] 1.423951
$ml_m
[1] 1
Call:
att_gt(yname = "Y", tname = "period", idname = "id", gname = "G",
xformla = ~X, data = dta, est_method = doubleml_did_eval_linear,
print_details = TRUE)
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
Group-Time Average Treatment Effects:
Group Time ATT(g,t) Std. Error [95% Simult. Conf. Band]
2 2 0.9145 0.0646 0.7368 1.0922 *
2 3 1.9951 0.0631 1.8215 2.1687 *
2 4 2.9561 0.0622 2.7850 3.1273 *
3 2 -0.0418 0.0629 -0.2147 0.1312
3 3 1.1041 0.0651 0.9251 1.2830 *
3 4 2.0533 0.0658 1.8725 2.2341 *
4 2 -0.0028 0.0718 -0.2002 0.1946
4 3 0.0635 0.0663 -0.1188 0.2458
4 4 0.9609 0.0690 0.7711 1.1507 *
---
Signif. codes: `*' confidence band does not cover 0
P-value for pre-test of parallel trends assumption: 0.64579
Control Group: Never Treated, Anticipation Periods: 0
[10]:
# Run estimation with evaluation: Linear model
set.seed(1234)
example_attgt_dml_eval_rf <- att_gt(yname = "Y",
tname = "period",
idname = "id",
gname = "G",
xformla = ~X,
data = dta,
est_method = doubleml_did_eval_rf,
print_details = TRUE)
summary(example_attgt_dml_eval_rf)
Evaluating (g,t) = (2,1)$ml_g0
[1] 1.571778
$ml_m
[1] 1
Evaluating (g,t) = (2,2)$ml_g0
[1] 1.916236
$ml_m
[1] 1
Evaluating (g,t) = (2,3)$ml_g0
[1] 2.404318
$ml_m
[1] 1
Evaluating (g,t) = (3,1)$ml_g0
[1] 1.570486
$ml_m
[1] 1
Evaluating (g,t) = (3,2)$ml_g0
[1] 1.529782
$ml_m
[1] 1
Evaluating (g,t) = (3,3)$ml_g0
[1] 1.88629
$ml_m
[1] 1
Evaluating (g,t) = (4,1)$ml_g0
[1] 1.570562
$ml_m
[1] 1
Evaluating (g,t) = (4,2)$ml_g0
[1] 1.529405
$ml_m
[1] 1
Evaluating (g,t) = (4,3)$ml_g0
[1] 1.560689
$ml_m
[1] 1
Call:
att_gt(yname = "Y", tname = "period", idname = "id", gname = "G",
xformla = ~X, data = dta, est_method = doubleml_did_eval_rf,
print_details = TRUE)
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
Group-Time Average Treatment Effects:
Group Time ATT(g,t) Std. Error [95% Simult. Conf. Band]
2 2 0.9647 0.0698 0.7733 1.1562 *
2 3 2.1055 0.0879 1.8643 2.3467 *
2 4 3.1295 0.1056 2.8397 3.4192 *
3 2 0.0820 0.0702 -0.1106 0.2747
3 3 1.2075 0.0704 1.0144 1.4006 *
3 4 2.2865 0.0889 2.0428 2.5302 *
4 2 0.1807 0.0713 -0.0149 0.3763
4 3 0.2451 0.0675 0.0599 0.4302 *
4 4 1.1401 0.0698 0.9485 1.3316 *
---
Signif. codes: `*' confidence band does not cover 0
P-value for pre-test of parallel trends assumption: 2e-05
Control Group: Never Treated, Anticipation Periods: 0
Acknowledgements and Final Remarks#
We’d like to thank the authors of the did package for R for maintaining a flexible interface for multi-period DiD models.
We’d like to note that the implementation presented is here is very similar to the one implemented in the Python package. For more details, we would like to reference to the DiD examples in Python.
References#
Callaway, Brantly, and Pedro HC Sant’Anna. “Difference-in-differences with multiple time periods.” Journal of Econometrics 225.2 (2021): 200-230.
Sant’Anna, Pedro HC, and Jun Zhao. “Doubly robust difference-in-differences estimators.” Journal of Econometrics 219.1 (2020): 101-122.

