Note
-
Download Jupyter notebook:
https://docs.doubleml.org/stable/examples/py_double_ml_policy_tree.ipynb.
Python: Policy Learning with Trees#
In this simple example, we illustrate how the DoubleML package can be used to estimate deterministic binary treatment policies.
Data#
The data will be generated with a simple data generating process to enable us to know the true policy cut-offs.
[1]:
import numpy as np
import pandas as pd
import doubleml as dml
Here, we consider a treatment effect that depends on two covariates which might correspond to opposite effects depending on age or income. For simplicity, the treatment effect within each group is generated to be constant.
[2]:
def group_effect(x):
if x[0] <= -0.3:
te = 2.2
elif (x[0] >= 0.2) & (x[1] >= 0.4):
te = 2
else:
te = -2
return te
The data is generated as
where \(W_i\sim\mathcal{N}(0,I_{d_w})\) and \(\epsilon_i,\eta_i\sim\mathcal{U}[0,1]\). The coefficient vectors \(\gamma_0\) and \(\beta_0\) both have small random support which values are drawn independently from \(\mathcal{U}[0,1]\). Further, \(g(w_1,w_2)\) defines the conditional treatment effect, which is generated depending on \(\{w_1,w_2\}\).
[3]:
def create_synthetic_group_data(n_samples=200, n_w=10, support_size=5):
"""
Creates a simple synthetic example for group effects.
Parameters
----------
n_samples : int
Number of samples.
Default is ``200``.
n_w : int
Dimension of covariates.
Default is ``10``.
support_size : int
Number of relevant covariates.
Default is ``5``.
Returns
-------
data : pd.DataFrame
A data frame.
"""
# Outcome support
support_w = np.random.choice(np.arange(n_w), size=support_size, replace=False)
coefs_w = np.random.uniform(0, 1, size=support_size)
# Define the function to generate the noise
epsilon_sample = lambda n: np.random.uniform(-1, 1, size=n_samples)
# Treatment support
# Assuming the matrices gamma and beta have the same number of non-zero components
support_t = np.random.choice(np.arange(n_w), size=support_size, replace=False)
coefs_t = np.random.uniform(0, 1, size=support_size)
# Define the function to generate the noise
eta_sample = lambda n: np.random.uniform(-1, 1, size=n_samples)
# Generate controls, covariates, treatments and outcomes
w = np.random.normal(0, 1, size=(n_samples, n_w))
# Group treatment effect
te = np.apply_along_axis(group_effect, axis=1, arr=w)
# Define treatment
log_odds = np.dot(w[:, support_t], coefs_t) + eta_sample(n_samples)
t_sigmoid = 1 / (1 + np.exp(-log_odds))
t = np.array([np.random.binomial(1, p) for p in t_sigmoid])
# Define the outcome
y = te * t + np.dot(w[:, support_w], coefs_w) + epsilon_sample(n_samples)
# Now we build the dataset
y_df = pd.DataFrame({'y': y})
t_df = pd.DataFrame({'t': t})
w_df = pd.DataFrame(data=w, index=np.arange(w.shape[0]),
columns=[f'w_{i}' for i in range(1, w.shape[1] + 1)])
data = pd.concat([y_df, t_df, w_df], axis=1)
covariates = list(w_df.columns.values)
return data, covariates
We will consider a quite small number of covariates to ensure fast calcualtion.
[4]:
# DGP constants
np.random.seed(42)
n_samples = 500
n_w = 10
support_size = 5
# Create data
data, covariates = create_synthetic_group_data(n_samples=n_samples, n_w=n_w, support_size=support_size)
data_dml_base = dml.DoubleMLData(data,
y_col='y',
d_cols='t',
x_cols=covariates)
Interactive Regression Model (IRM)#
The first step is to fit a DoubleML IRM Model to the data.
[5]:
# First stage estimation
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
randomForest_reg = RandomForestRegressor(n_estimators=200, random_state=42)
randomForest_class = RandomForestClassifier(n_estimators=200, random_state=42)
np.random.seed(42)
dml_irm = dml.DoubleMLIRM(data_dml_base,
ml_g=randomForest_reg,
ml_m=randomForest_class,
trimming_threshold=0.01,
n_folds=5)
print("Training IRM Model")
dml_irm.fit(store_predictions=True)
Training IRM Model
[5]:
<doubleml.double_ml_irm.DoubleMLIRM at 0x2920d7b7150>
Policy Learning with Trees#
Next, we specify the covariates as a DataFrame against which to learn the policy. This can either be all covariates \(w_i\), or if domain knowledge is available we can use a subset.
[6]:
features = data[["w_1","w_2"]].copy()
print(features)
w_1 w_2
0 -0.428046 -0.742407
1 -0.600254 0.947440
2 -1.265119 1.091992
3 -1.346678 -0.880591
4 -1.508153 1.099647
.. ... ...
495 -2.072293 -0.951920
496 0.144908 0.280963
497 -0.877455 -2.404550
498 -0.981104 -0.830301
499 -0.555445 0.021866
[500 rows x 2 columns]
To estimate a Policy just call the policy_tree() method and supply the DataFrame with the features and the depth of the desired tree.
[7]:
policy_tree = dml_irm.policy_tree(features=features, depth=3)
policy_tree.plot_tree();
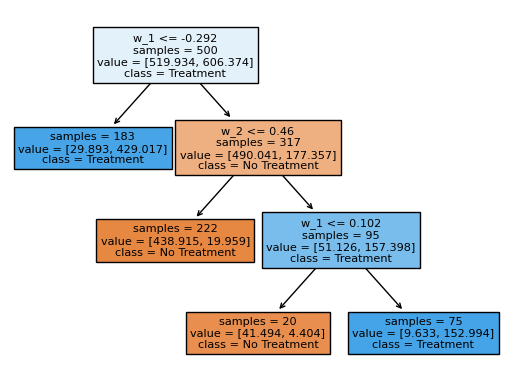
The splits in this classification tree reflect the heterogeneity in the data generating process above. Exemplatory, we see that the first split is estimated at \(w_1 = -0.292\). In the DGP, at \(w_1 = -0.3\) the treatment effect jumps from \(-2\) to \(2.2\).
Alternatively, it is also possible to estimate the tree on all covariates, which in this case results in the same splits.
[8]:
policy_tree_2 = dml_irm.policy_tree(features=data[covariates], depth=3)
policy_tree_2.plot_tree();
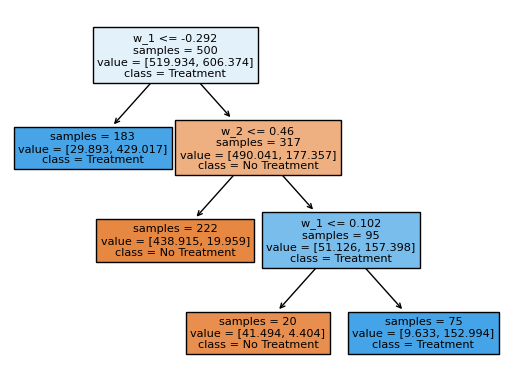
The policytree predict() method is useful to estimate the optimal treatments on new data.
[9]:
new_data, _ = create_synthetic_group_data(n_samples=n_samples, n_w=n_w, support_size=support_size)
pred_df = policy_tree.predict(features=new_data[["w_1","w_2"]])
print(pred_df)
w_1 w_2 pred_treatment
0 -1.155516 1.570111 1
1 -2.216761 1.389566 1
2 0.764478 -1.111164 0
3 -0.411291 0.984024 1
4 0.324518 1.675293 1
.. ... ... ...
495 -1.728294 -0.018023 1
496 0.632958 2.557731 1
497 -0.161198 0.661369 0
498 0.351766 0.523807 1
499 -0.366529 1.310761 1
[500 rows x 3 columns]
These predicted optimal treatments maximize the overall Average Treament Effect on the treated within the new data. We showcase that with the help of the gate() method.
[10]:
data_dml_new = dml.DoubleMLData(new_data,
y_col="y",
d_cols="t")
dml_irm_new = dml.DoubleMLIRM(data_dml_new,
ml_g=randomForest_reg,
ml_m=randomForest_class,
trimming_threshold=0.01,
n_folds=5)
dml_irm_new.fit()
print("ATTE under the original treatment policy:")
print(dml_irm_new.gate(groups=new_data["t"].to_frame()).confint())
print("\nATTE under the estimated optimal treatment policy:")
print(dml_irm_new.gate(groups=pred_df["pred_treatment"].to_frame()).confint())
ATTE under the original treatment policy:
2.5 % effect 97.5 %
t -0.192505 0.177463 0.547431
ATTE under the estimated optimal treatment policy:
2.5 % effect 97.5 %
pred_treatment 1.712157 1.982797 2.253437
Using the original policy in the underlying DGP, we achieve a significant ATTE improvement.