R: Basic Instrumental Variables Calculation#

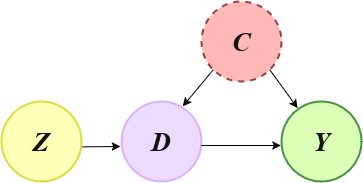
In this example we show how to use the DoubleML functionality of Instrumental Variables (IVs) in the basic setting shown in the graph below, where:

Z is the instrument
C is a vector of unobserved confounders
D is the decision or treatment variable
Y is the outcome

So, we will first generate synthetic data using linear models compatible with the diagram, and then use the DoubleML package to estimate the causal effect from D to Y.

We assume that you have basic knowledge of instrumental variables and linear regression.

[1]:

library(DoubleML)
library(mlr3learners)

set.seed(1234)
options(warn=-1)

Loading required package: mlr3

Instrumental Variables Directed Acyclic Graph (IV - DAG)#

Data Simulation#

This code generates n samples in which there is a unique binary confounder. The treatment is also a binary variable, while the outcome is a continuous linear model.

The quantity we want to recover using IVs is the decision_impact, which is the impact of the decision variable into the outcome.

[2]:

n <- 10000
decision_effect <- -2
instrument_effect <- 0.7

confounder <- rbinom(n, 1, 0.3)
instrument <- rbinom(n, 1, 0.5)
decision <- as.numeric(runif(n) <= instrument_effect*instrument + 0.4*confounder)
outcome <- 30 + decision_effect*decision + 10 * confounder + rnorm(n, sd=2)
df <- data.frame(instrument, decision, outcome)

Naive estimation#

We can see that if we make a direct estimation of the impact of the decision into the outcome, though the difference of the averages of outcomes between the two decision groups, we obtain a biased estimate.

[3]:

mean(df[df$decision==1, 'outcome']) - mean(df[df$decision==0, 'outcome'])

1.00047580260495

Using DoubleML#

DoubleML assumes that there is at least one observed confounder. For this reason, we create a fake variable that doesn’t bring any kind of information to the model, called obs_confounder.

To use the DoubleML we need to specify the Machine Learning methods we want to use to estimate the different relationships between variables:

ml_g models the functional relationship betwen the outcome and the pair instrument and observed confounders obs_confounders. In this case we choose a LinearRegression because the outcome is continuous.
ml_m models the functional relationship betwen the obs_confounders and the instrument. In this case we choose a LogisticRegression because the outcome is dichotomic.
ml_r models the functional relationship betwen the decision and the pair instrument and observed confounders obs_confounders. In this case we choose a LogisticRegression because the outcome is dichotomic.

Notice that instead of using linear and logistic regression, we could use more flexible models capable of dealing with non-linearities such as random forests, boosting, …

[4]:

df['obs_confounders'] <- 1

obj_dml_data = DoubleMLData$new(
  df, y_col="outcome", d_col = "decision",
  z_cols= "instrument", x_cols = "obs_confounders"
)

ml_g = lrn("regr.lm")
ml_m = lrn("classif.log_reg")
ml_r = ml_m$clone()

iv_2 = DoubleMLIIVM$new(obj_dml_data, ml_g, ml_m, ml_r)
result <- iv_2$fit()

INFO  [09:43:39.120] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_m' (iter 1/5)
INFO  [09:43:39.375] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_m' (iter 2/5)
INFO  [09:43:39.416] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_m' (iter 3/5)
INFO  [09:43:39.457] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_m' (iter 4/5)
INFO  [09:43:39.499] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_m' (iter 5/5)
INFO  [09:43:39.595] [mlr3] Applying learner 'regr.lm' on task 'nuis_g0' (iter 1/5)
INFO  [09:43:39.612] [mlr3] Applying learner 'regr.lm' on task 'nuis_g0' (iter 2/5)
INFO  [09:43:39.628] [mlr3] Applying learner 'regr.lm' on task 'nuis_g0' (iter 3/5)
INFO  [09:43:39.644] [mlr3] Applying learner 'regr.lm' on task 'nuis_g0' (iter 4/5)
INFO  [09:43:39.669] [mlr3] Applying learner 'regr.lm' on task 'nuis_g0' (iter 5/5)
INFO  [09:43:39.734] [mlr3] Applying learner 'regr.lm' on task 'nuis_g1' (iter 1/5)
INFO  [09:43:39.749] [mlr3] Applying learner 'regr.lm' on task 'nuis_g1' (iter 2/5)
INFO  [09:43:39.765] [mlr3] Applying learner 'regr.lm' on task 'nuis_g1' (iter 3/5)
INFO  [09:43:39.781] [mlr3] Applying learner 'regr.lm' on task 'nuis_g1' (iter 4/5)
INFO  [09:43:39.800] [mlr3] Applying learner 'regr.lm' on task 'nuis_g1' (iter 5/5)
INFO  [09:43:39.869] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r0' (iter 1/5)
INFO  [09:43:39.898] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r0' (iter 2/5)
INFO  [09:43:39.930] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r0' (iter 3/5)
INFO  [09:43:39.957] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r0' (iter 4/5)
INFO  [09:43:39.994] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r0' (iter 5/5)
INFO  [09:43:40.071] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r1' (iter 1/5)
INFO  [09:43:40.102] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r1' (iter 2/5)
INFO  [09:43:40.129] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r1' (iter 3/5)
INFO  [09:43:40.155] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r1' (iter 4/5)
INFO  [09:43:40.185] [mlr3] Applying learner 'classif.log_reg' on task 'nuis_r1' (iter 5/5)

[5]:

result

================= DoubleMLIIVM Object ==================


------------------ Data summary      ------------------
Outcome variable: outcome
Treatment variable(s): decision
Covariates: obs_confounders
Instrument(s): instrument
No. Observations: 10000

------------------ Score & algorithm ------------------
Score function: LATE
DML algorithm: dml2

------------------ Machine learner   ------------------
ml_g: regr.lm
ml_m: classif.log_reg
ml_r: classif.log_reg

------------------ Resampling        ------------------
No. folds: 5
No. repeated sample splits: 1
Apply cross-fitting: TRUE

------------------ Fit summary       ------------------
 Estimates and significance testing of the effect of target variables
         Estimate. Std. Error t value Pr(>|t|)
decision   -1.8904     0.1492  -12.67   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

We can see that the causal effect is estimated without bias.

References#

Ruiz de Villa, A. Causal Inference for Data Science, Manning Publications, 2024.