Note
-
Download Jupyter notebook:
https://docs.doubleml.org/stable/examples/did/py_rep_cs.ipynb.
Python: Repeated Cross-Sectional Data with Multiple Time Periods#
In this example, a detailed guide on Difference-in-Differences with multiple time periods using the DoubleML-package. The implementation is based on Callaway and Sant’Anna(2021).
The notebook requires the following packages:
[1]:
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from lightgbm import LGBMRegressor, LGBMClassifier
from sklearn.linear_model import LinearRegression, LogisticRegression
from doubleml.did import DoubleMLDIDMulti
from doubleml.data import DoubleMLPanelData
from doubleml.did.datasets import make_did_cs_CS2021
Data#
We will rely on the make_did_cs_CS2021 DGP, which is inspired by Callaway and Sant’Anna(2021) (Appendix SC) and Sant’Anna and Zhao (2020).
We will observe approximately n_obs units over n_periods. The parameter lambda_t determines the probability of observing a unit i in time period t. The parameter lambda_t is set to 0.5 for all time periods, which means that each unit has a 50% chance of being observed in each time period.
Remark that the dataframe includes observations of the potential outcomes y0 and y1, such that we can use oracle estimates as comparisons.
[2]:
n_obs = 10000
n_periods = 6
df = make_did_cs_CS2021(n_obs, dgp_type=4, include_never_treated=True, n_periods=n_periods, n_pre_treat_periods=3,
lambda_t=0.5, time_type="float")
df["ite"] = df["y1"] - df["y0"]
print(df.shape)
df.head()
(60296, 11)
[2]:
| id | y | y0 | y1 | d | t | Z1 | Z2 | Z3 | Z4 | ite | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 206.042008 | 206.042008 | 207.562116 | inf | 0 | -0.479727 | 0.086133 | 0.777112 | 0.348720 | 1.520108 |
| 1 | 0 | 201.553117 | 201.553117 | 201.579717 | inf | 1 | -0.479727 | 0.086133 | 0.777112 | 0.348720 | 0.026600 |
| 3 | 0 | 191.849890 | 191.849890 | 191.552489 | inf | 3 | -0.479727 | 0.086133 | 0.777112 | 0.348720 | -0.297401 |
| 4 | 0 | 187.743850 | 187.743850 | 188.572793 | inf | 4 | -0.479727 | 0.086133 | 0.777112 | 0.348720 | 0.828943 |
| 9 | 1 | 255.621101 | 255.621101 | 255.976198 | 5.0 | 3 | 1.199114 | 0.148871 | 1.203296 | 0.664904 | 0.355097 |
Data Details#
Here, we slightly abuse the definition of the potential outcomes. :math:`Y_{i,t}(1)` corresponds to the (potential) outcome if unit :math:`i` would have received treatment at time period :math:`mathrm{g}` (where the group :math:`mathrm{g}` is drawn with probabilities based on :math:`Z`).
The data set with repeated cross-sectional data is generated on the basis of a panel data set with the following data generating process (DGP). To obtain repeated cross-sectional data, the number of generated individuals is increased to \(\frac{n_{obs}}{\lambda_t}\), where \(\lambda_t\) denotes the probability to observe a unit at each time period (time constant).
More specifically
where
\(f_t(Z)\) depends on pre-treatment observable covariates \(Z_1,\dots, Z_4\) and time \(t\)
\(\delta_t\) is a time fixed effect
\(\eta_i\) is a unit fixed effect
\(\epsilon_{i,t,\cdot}\) are time varying unobservables (iid. \(N(0,1)\))
\(\theta_{i,t,\mathrm{g}}\) correponds to the exposure effect of unit \(i\) based on group \(\mathrm{g}\) at time \(t\)
For the pre-treatment periods the exposure effect is set to
such that
The DoubleML Coverage Repository includes coverage simulations based on this DGP.
Data Description#
The data is a balanced panel where each unit is observed over n_periods starting Janary 2025.
[3]:
df.groupby("t").size()
[3]:
t
0 10022
1 10061
2 10063
3 10041
4 10104
5 10005
dtype: int64
The treatment column d indicates first treatment period of the corresponding unit, whereas NaT units are never treated.
Generally, never treated units should take either on the value ``np.inf`` or ``pd.NaT`` depending on the data type (``float`` or ``datetime``).
The individual units are roughly uniformly divided between the groups, where treatment assignment depends on the pre-treatment covariates Z1 to Z4.
[4]:
df.groupby("d", dropna=False).size()
[4]:
d
3.0 15552
4.0 14628
5.0 14732
inf 15384
dtype: int64
Here, the group indicates the first treated period and NaT units are never treated. To simplify plotting and pands
[5]:
df.groupby("d", dropna=False).size()
[5]:
d
3.0 15552
4.0 14628
5.0 14732
inf 15384
dtype: int64
To get a better understanding of the underlying data and true effects, we will compare the unconditional averages and the true effects based on the oracle values of individual effects ite.
[6]:
# rename for plotting
# Create aggregation dictionary for means
def agg_dict(col_name):
return {
f'{col_name}_mean': (col_name, 'mean'),
f'{col_name}_lower_quantile': (col_name, lambda x: x.quantile(0.05)),
f'{col_name}_upper_quantile': (col_name, lambda x: x.quantile(0.95))
}
# Calculate means and confidence intervals
agg_dictionary = agg_dict("y") | agg_dict("ite")
agg_df = df.groupby(["t", "d"]).agg(**agg_dictionary).reset_index()
agg_df.head()
[6]:
| t | d | y_mean | y_lower_quantile | y_upper_quantile | ite_mean | ite_lower_quantile | ite_upper_quantile | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3.0 | 208.751116 | 198.899093 | 218.536500 | 0.046519 | -2.312490 | 2.391797 |
| 1 | 0 | 4.0 | 210.518674 | 200.545900 | 220.739513 | -0.009747 | -2.267687 | 2.213630 |
| 2 | 0 | 5.0 | 212.548293 | 202.419314 | 222.712593 | -0.028158 | -2.236719 | 2.276548 |
| 3 | 0 | inf | 214.125497 | 203.785276 | 224.036455 | -0.068083 | -2.388256 | 2.322986 |
| 4 | 1 | 3.0 | 208.871288 | 189.101515 | 228.416654 | -0.010209 | -2.397847 | 2.272665 |
[7]:
def plot_data(df, col_name='y'):
"""
Create an improved plot with colorblind-friendly features
Parameters:
-----------
df : DataFrame
The dataframe containing the data
col_name : str, default='y'
Column name to plot (will use '{col_name}_mean')
"""
plt.figure(figsize=(12, 7))
n_colors = df["d"].nunique()
color_palette = sns.color_palette("colorblind", n_colors=n_colors)
sns.lineplot(
data=df,
x='t',
y=f'{col_name}_mean',
hue='d',
style='d',
palette=color_palette,
markers=True,
dashes=True,
linewidth=2.5,
alpha=0.8
)
plt.title(f'Average Values {col_name} by Group Over Time', fontsize=16)
plt.xlabel('Time', fontsize=14)
plt.ylabel(f'Average Value {col_name}', fontsize=14)
plt.legend(title='d', title_fontsize=13, fontsize=12,
frameon=True, framealpha=0.9, loc='best')
plt.grid(alpha=0.3, linestyle='-')
plt.tight_layout()
plt.show()
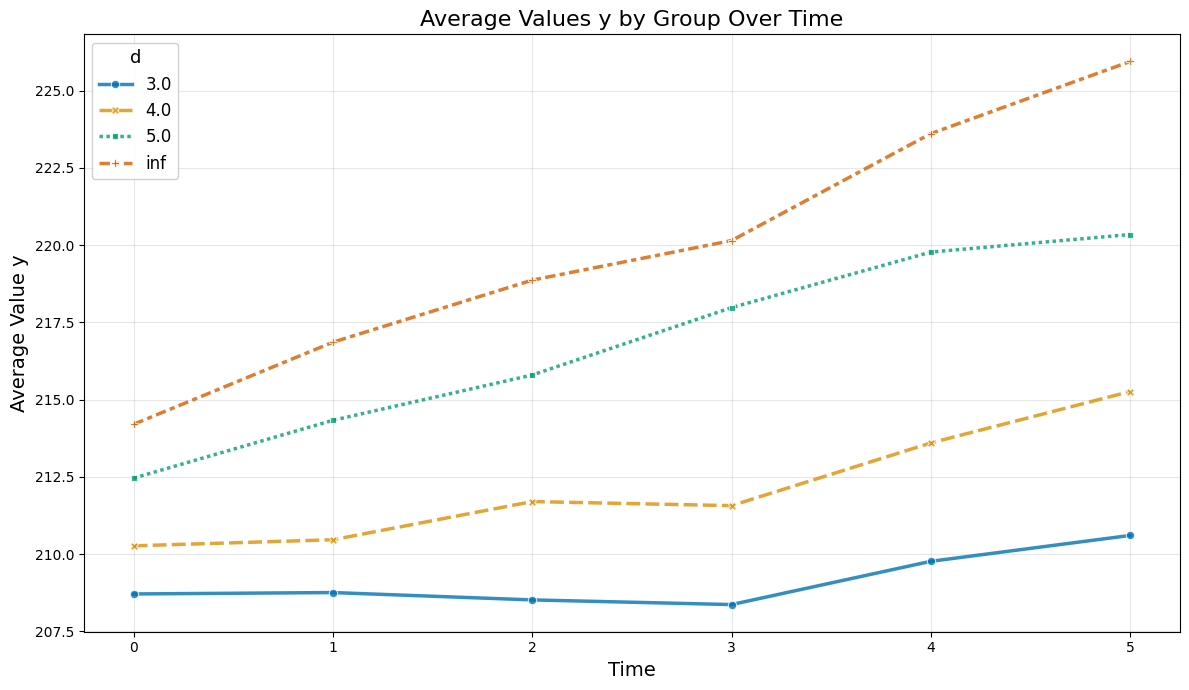
So let us take a look at the average values over time
[8]:
plot_data(agg_df, col_name='y')
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/colors.py:2295: RuntimeWarning: invalid value encountered in divide
resdat /= (vmax - vmin)
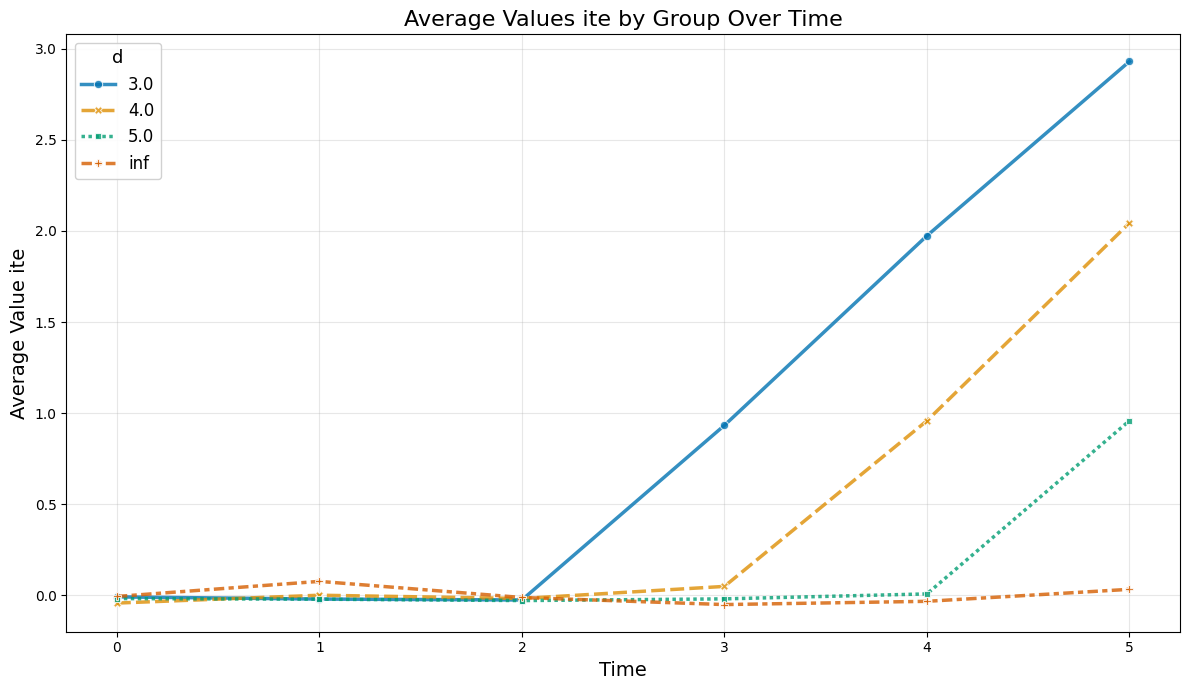
Instead the true average treatment treatment effects can be obtained by averaging (usually unobserved) the ite values.
The true effect just equals the exposure time (in months):
[9]:
plot_data(agg_df, col_name='ite')
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/colors.py:2295: RuntimeWarning: invalid value encountered in divide
resdat /= (vmax - vmin)
DoubleMLPanelData#
Finally, we can construct our DoubleMLPanelData, specifying
y_col: the outcomed_cols: the group variable indicating the first treated period for each unitid_col: the unique identification column for each unitt_col: the time columnx_cols: the additional pre-treatment controlsdatetime_unit: unit required fordatetimecolumns and plotting
[10]:
dml_data = DoubleMLPanelData(
data=df,
y_col="y",
d_cols="d",
id_col="id",
t_col="t",
x_cols=["Z1", "Z2", "Z3", "Z4"],
)
print(dml_data)
================== DoubleMLPanelData Object ==================
------------------ Data summary ------------------
Outcome variable: y
Treatment variable(s): ['d']
Covariates: ['Z1', 'Z2', 'Z3', 'Z4']
Instrument variable(s): None
Time variable: t
Id variable: id
Static panel data: False
No. Unique Ids: 19704
No. Observations: 60296
------------------ DataFrame info ------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 60296 entries, 0 to 60295
Columns: 11 entries, id to ite
dtypes: float64(9), int64(2)
memory usage: 5.1 MB
ATT Estimation#
The DoubleML-package implements estimation of group-time average treatment effect via the DoubleMLDIDMulti class (see model documentation).
Basics#
The class basically behaves like other DoubleML classes and requires the specification of two learners (for more details on the regression elements, see score documentation).
The basic arguments of a DoubleMLDIDMulti object include
ml_g“outcome” regression learnerml_mpropensity Score learnercontrol_groupthe control group for the parallel trend assumptiongt_combinationscombinations of \((\mathrm{g},t_\text{pre}, t_\text{eval})\)anticipation_periodsnumber of anticipation periods
We will construct a dict with “default” arguments.
For repeated cross-sectional data, we additionally specify the argument
panel=False
[11]:
default_args = {
"ml_g": LGBMRegressor(n_estimators=500, learning_rate=0.01, verbose=-1, random_state=123),
"ml_m": LGBMClassifier(n_estimators=500, learning_rate=0.01, verbose=-1, random_state=123),
"control_group": "never_treated",
"anticipation_periods": 0,
"n_folds": 5,
"n_rep": 1,
"panel": False,
}
The model will be estimated using the fit() method.
[12]:
dml_obj = DoubleMLDIDMulti(dml_data, **default_args)
dml_obj.fit()
print(dml_obj)
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
================== DoubleMLDIDMulti Object ==================
------------------ Data summary ------------------
Outcome variable: y
Treatment variable(s): ['d']
Covariates: ['Z1', 'Z2', 'Z3', 'Z4']
Instrument variable(s): None
Time variable: t
Id variable: id
Static panel data: False
No. Unique Ids: 19704
No. Observations: 60296
------------------ Score & algorithm ------------------
Score function: observational
Control group: never_treated
Anticipation periods: 0
------------------ Machine learner ------------------
Learner ml_g: LGBMRegressor(learning_rate=0.01, n_estimators=500, random_state=123,
verbose=-1)
Learner ml_m: LGBMClassifier(learning_rate=0.01, n_estimators=500, random_state=123,
verbose=-1)
Out-of-sample Performance:
Regression:
Learner ml_g_d0_t0 RMSE: [[1.77635053 2.5354922 3.26153755 3.20993102 3.28200959 1.74540088
2.58410126 3.29456362 4.07649046 4.07412098 1.7445544 2.54731697
3.31224798 4.07606903 5.19864486]]
Learner ml_g_d0_t1 RMSE: [[2.49945849 3.20385232 4.11048699 5.31445965 5.87381478 2.51448941
3.2500049 4.12102445 5.18749684 6.08759754 2.54796266 3.30304123
4.18237874 5.25281993 6.14483146]]
Learner ml_g_d1_t0 RMSE: [[1.84778521 2.59353096 3.48043094 3.48578242 3.46535749 1.78009026
2.52323135 3.50248328 4.46097247 4.37141953 1.76739663 2.49116778
3.31006085 4.48387124 5.29469855]]
Learner ml_g_d1_t1 RMSE: [[2.59530545 3.49309297 4.35972833 5.54144842 6.38547613 2.52457394
3.50632619 4.40100715 5.22635246 6.46537548 2.45711778 3.284458
4.38000667 5.24108745 6.1991079 ]]
Classification:
Learner ml_m Log Loss: [[0.63045137 0.62593955 0.62609044 0.62265405 0.62557662 0.65178022
0.64840355 0.64986404 0.65186391 0.65026736 0.66910913 0.67138418
0.66687613 0.6673984 0.67045661]]
------------------ Resampling ------------------
No. folds: 5
No. repeated sample splits: 1
------------------ Fit summary ------------------
coef std err t P>|t| 2.5 % 97.5 %
ATT(3.0,0,1) -0.234497 0.109255 -2.146326 3.184695e-02 -0.448633 -0.020361
ATT(3.0,1,2) 0.276271 0.145513 1.898593 5.761803e-02 -0.008930 0.561471
ATT(3.0,2,3) 0.674924 0.220866 3.055802 2.244593e-03 0.242034 1.107815
ATT(3.0,2,4) 1.867589 0.278527 6.705231 2.010880e-11 1.321686 2.413492
ATT(3.0,2,5) 2.706101 0.247841 10.918707 0.000000e+00 2.220342 3.191860
ATT(4.0,0,1) -0.107650 0.102244 -1.052879 2.923966e-01 -0.308045 0.092744
ATT(4.0,1,2) 0.088173 0.133332 0.661300 5.084197e-01 -0.173154 0.349499
ATT(4.0,2,3) -0.336062 0.189029 -1.777833 7.543123e-02 -0.706552 0.034428
ATT(4.0,3,4) 1.473297 0.228347 6.452023 1.103666e-10 1.025746 1.920848
ATT(4.0,3,5) 2.253077 0.241215 9.340524 0.000000e+00 1.780304 2.725850
ATT(5.0,0,1) -0.019087 0.093422 -0.204308 8.381128e-01 -0.202191 0.164017
ATT(5.0,1,2) 0.085728 0.126182 0.679397 4.968865e-01 -0.161585 0.333041
ATT(5.0,2,3) -0.242083 0.162478 -1.489938 1.362405e-01 -0.560535 0.076369
ATT(5.0,3,4) 0.274516 0.205445 1.336198 1.814847e-01 -0.128150 0.677181
ATT(5.0,4,5) 0.872390 0.243406 3.584099 3.382437e-04 0.395324 1.349456
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
The summary displays estimates of the \(ATT(g,t_\text{eval})\) effects for different combinations of \((g,t_\text{eval})\) via \(\widehat{ATT}(\mathrm{g},t_\text{pre},t_\text{eval})\), where
\(\mathrm{g}\) specifies the group
\(t_\text{pre}\) specifies the corresponding pre-treatment period
\(t_\text{eval}\) specifies the evaluation period
The choice gt_combinations="standard", used estimates all possible combinations of \(ATT(g,t_\text{eval})\) via \(\widehat{ATT}(\mathrm{g},t_\text{pre},t_\text{eval})\), where the standard choice is \(t_\text{pre} = \min(\mathrm{g}, t_\text{eval}) - 1\) (without anticipation).
Remark that this includes pre-tests effects if \(\mathrm{g} > t_{eval}\), e.g. \(\widehat{ATT}(g=3, t_{\text{pre}}=0, t_{\text{eval}}=1)\) which estimates the pre-trend from time period \(0\) to \(1\) even if the actual treatment occured in time period \(3\).
As usual for the DoubleML-package, you can obtain joint confidence intervals via bootstrap.
[13]:
level = 0.95
ci = dml_obj.confint(level=level)
dml_obj.bootstrap(n_rep_boot=5000)
ci_joint = dml_obj.confint(level=level, joint=True)
ci_joint
[13]:
| 2.5 % | 97.5 % | |
|---|---|---|
| ATT(3.0,0,1) | -0.550857 | 0.081863 |
| ATT(3.0,1,2) | -0.145080 | 0.697621 |
| ATT(3.0,2,3) | 0.035380 | 1.314468 |
| ATT(3.0,2,4) | 1.061082 | 2.674096 |
| ATT(3.0,2,5) | 1.988450 | 3.423752 |
| ATT(4.0,0,1) | -0.403709 | 0.188408 |
| ATT(4.0,1,2) | -0.297906 | 0.474251 |
| ATT(4.0,2,3) | -0.883417 | 0.211293 |
| ATT(4.0,3,4) | 0.812094 | 2.134500 |
| ATT(4.0,3,5) | 1.554611 | 2.951543 |
| ATT(5.0,0,1) | -0.289601 | 0.251427 |
| ATT(5.0,1,2) | -0.279647 | 0.451103 |
| ATT(5.0,2,3) | -0.712558 | 0.228392 |
| ATT(5.0,3,4) | -0.320375 | 0.869406 |
| ATT(5.0,4,5) | 0.167581 | 1.577198 |
A visualization of the effects can be obtained via the plot_effects() method.
Remark that the plot used joint confidence intervals per default.
[14]:
dml_obj.plot_effects()
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
[14]:
(<Figure size 1200x800 with 4 Axes>,
[<Axes: title={'center': 'First Treated: 3.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 4.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 5.0'}, xlabel='Evaluation Period', ylabel='Effect'>])
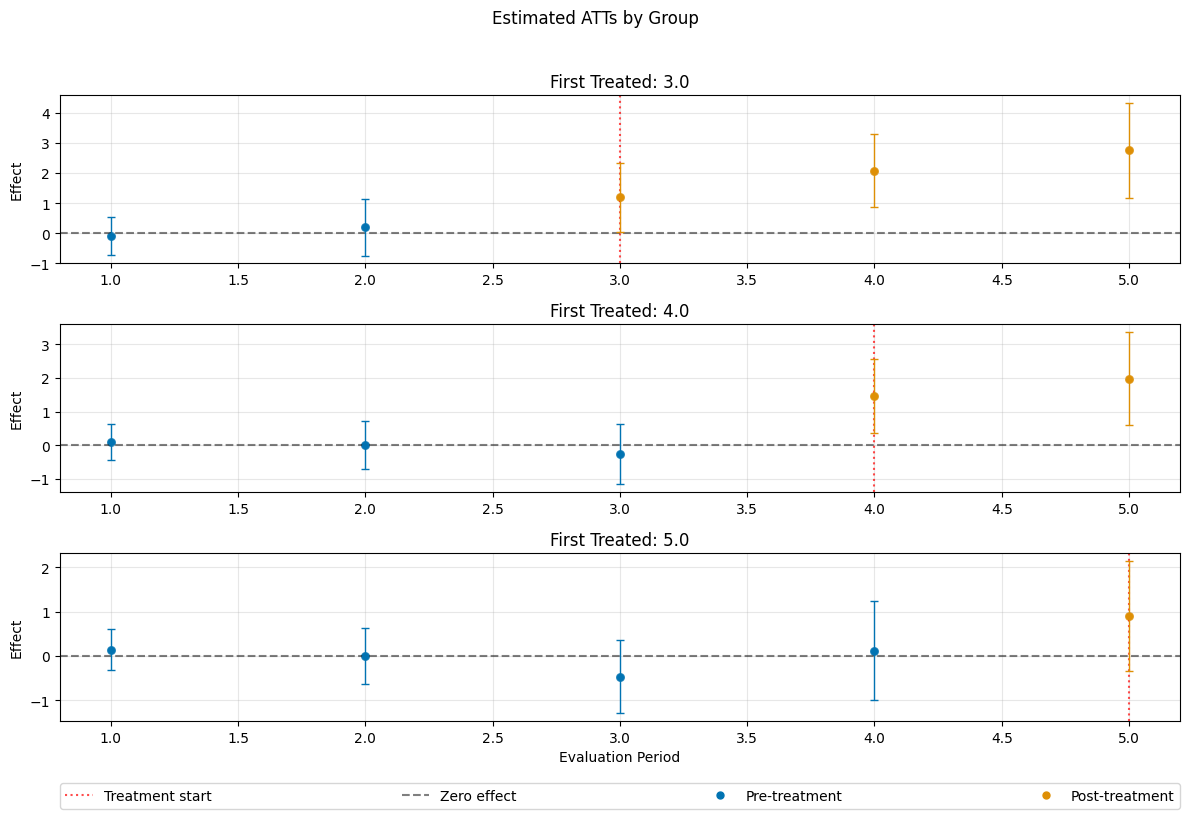
Sensitivity Analysis#
As descripted in the Sensitivity Guide, robustness checks on omitted confounding/parallel trend violations are available, via the standard sensitivity_analysis() method.
[15]:
dml_obj.sensitivity_analysis()
print(dml_obj.sensitivity_summary)
================== Sensitivity Analysis ==================
------------------ Scenario ------------------
Significance Level: level=0.95
Sensitivity parameters: cf_y=0.03; cf_d=0.03, rho=1.0
------------------ Bounds with CI ------------------
CI lower theta lower theta theta upper CI upper
ATT(3.0,0,1) -0.731915 -0.550591 -0.234497 0.081597 0.260423
ATT(3.0,1,2) -0.394724 -0.153875 0.276271 0.706416 0.945859
ATT(3.0,2,3) -0.219816 0.145645 0.674924 1.204203 1.567718
ATT(3.0,2,4) 0.781254 1.233763 1.867589 2.501415 2.968037
ATT(3.0,2,5) 1.587334 1.992245 2.706101 3.419957 3.832777
ATT(4.0,0,1) -0.564170 -0.395533 -0.107650 0.180232 0.348385
ATT(4.0,1,2) -0.528073 -0.307611 0.088173 0.483956 0.702976
ATT(4.0,2,3) -1.158922 -0.848474 -0.336062 0.176350 0.488689
ATT(4.0,3,4) 0.466706 0.842865 1.473297 2.103730 2.479932
ATT(4.0,3,5) 1.132513 1.529824 2.253077 2.976329 3.373918
ATT(5.0,0,1) -0.450620 -0.296440 -0.019087 0.258266 0.411813
ATT(5.0,1,2) -0.495666 -0.286877 0.085728 0.458332 0.665267
ATT(5.0,2,3) -1.001239 -0.733537 -0.242083 0.249372 0.516915
ATT(5.0,3,4) -0.683252 -0.343658 0.274516 0.892690 1.229920
ATT(5.0,4,5) -0.261463 0.138563 0.872390 1.606217 2.008070
------------------ Robustness Values ------------------
H_0 RV (%) RVa (%)
ATT(3.0,0,1) 0.0 2.234430 0.528491
ATT(3.0,1,2) 0.0 1.937445 0.260658
ATT(3.0,2,3) 0.0 3.809583 1.771783
ATT(3.0,2,4) 0.0 8.581512 6.586099
ATT(3.0,2,5) 0.0 10.899648 9.338639
ATT(4.0,0,1) 0.0 1.132697 0.000467
ATT(4.0,1,2) 0.0 0.676453 0.000354
ATT(4.0,2,3) 0.0 1.977970 0.148969
ATT(4.0,3,4) 0.0 6.869634 5.157080
ATT(4.0,3,5) 0.0 9.049428 7.502324
ATT(5.0,0,1) 0.0 0.209251 0.000484
ATT(5.0,1,2) 0.0 0.698528 0.000342
ATT(5.0,2,3) 0.0 1.489336 0.000461
ATT(5.0,3,4) 0.0 1.343677 0.000504
ATT(5.0,4,5) 0.0 3.556280 1.941788
In this example one can clearly, distinguish the robustness of the non-zero effects vs. the pre-treatment periods.
Control Groups#
The current implementation support the following control groups
"never_treated""not_yet_treated"
Remark that the ``”not_yet_treated” depends on anticipation.
For differences and recommendations, we refer to Callaway and Sant’Anna(2021).
[16]:
dml_obj_nyt = DoubleMLDIDMulti(dml_data, **(default_args | {"control_group": "not_yet_treated"}))
dml_obj_nyt.fit()
dml_obj_nyt.bootstrap(n_rep_boot=5000)
dml_obj_nyt.plot_effects()
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
[16]:
(<Figure size 1200x800 with 4 Axes>,
[<Axes: title={'center': 'First Treated: 3.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 4.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 5.0'}, xlabel='Evaluation Period', ylabel='Effect'>])
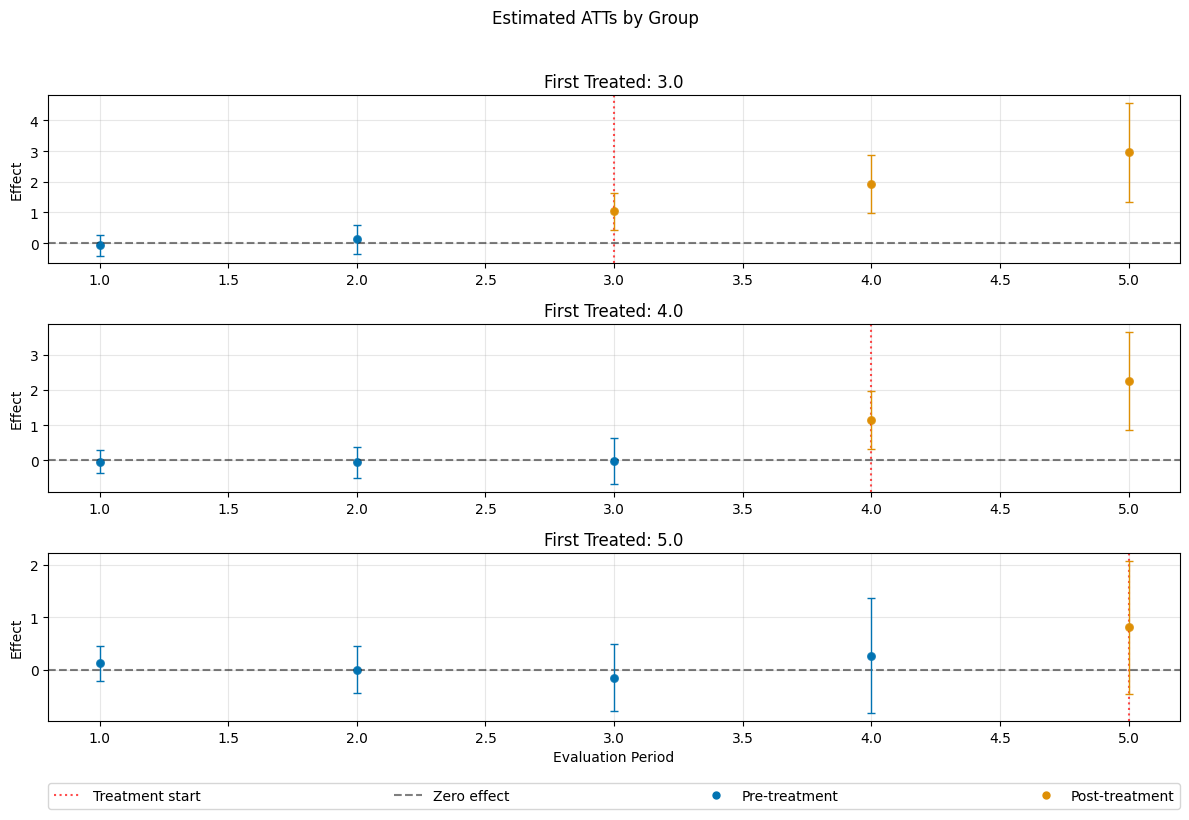
Linear Covariate Adjustment#
Remark that we relied on boosted trees to adjust for conditional parallel trends which allow for a nonlinear adjustment. In comparison to linear adjustment, we could rely on linear learners.
Remark that the DGP (``dgp_type=4``) is based on nonlinear conditional expectations such that the estimates will be biased
[17]:
linear_learners = {
"ml_g": LinearRegression(),
"ml_m": LogisticRegression(),
}
dml_obj_linear = DoubleMLDIDMulti(dml_data, **(default_args | linear_learners))
dml_obj_linear.fit()
dml_obj_linear.bootstrap(n_rep_boot=5000)
dml_obj_linear.plot_effects()
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
[17]:
(<Figure size 1200x800 with 4 Axes>,
[<Axes: title={'center': 'First Treated: 3.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 4.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 5.0'}, xlabel='Evaluation Period', ylabel='Effect'>])
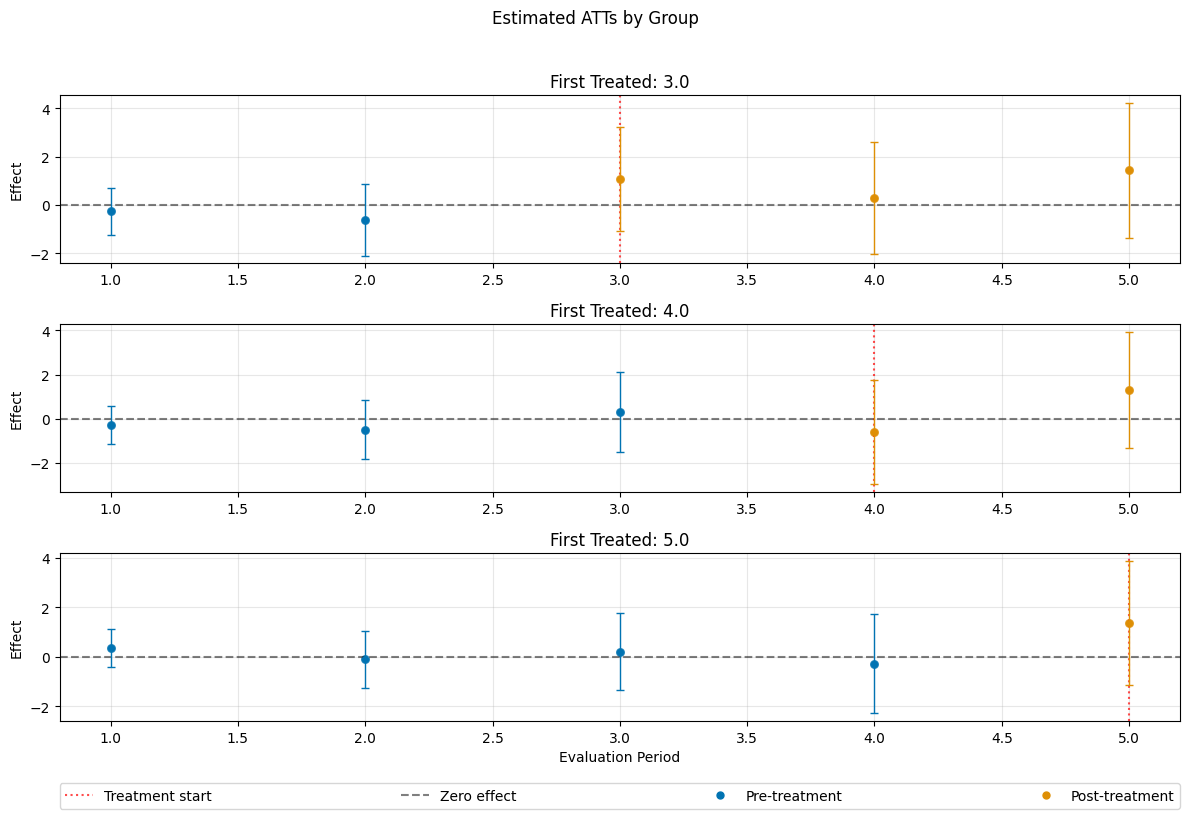
Aggregated Effects#
As the did-R-package, the \(ATT\)’s can be aggregated to summarize multiple effects. For details on different aggregations and details on their interpretations see Callaway and Sant’Anna(2021).
The aggregations are implemented via the aggregate() method.
Group Aggregation#
To obtain group-specific effects one can would like to average \(ATT(\mathrm{g}, t_\text{eval})\) over \(t_\text{eval}\). As a sample oracle we will combine all ite’s based on group \(\mathrm{g}\).
[18]:
df_post_treatment = df[df["t"] >= df["d"]]
df_post_treatment.groupby("d")["ite"].mean()
[18]:
d
3.0 1.936037
4.0 1.472415
5.0 0.965246
Name: ite, dtype: float64
To obtain group-specific effects it is possible to aggregate several \(\widehat{ATT}(\mathrm{g},t_\text{pre},t_\text{eval})\) values based on the group \(\mathrm{g}\) by setting the aggregation="group" argument.
[19]:
aggregated_group = dml_obj.aggregate(aggregation="group")
print(aggregated_group)
_ = aggregated_group.plot_effects()
================== DoubleMLDIDAggregation Object ==================
Group Aggregation
------------------ Overall Aggregated Effects ------------------
coef std err t P>|t| 2.5 % 97.5 %
1.498832 0.121412 12.345037 0.0 1.26087 1.736795
------------------ Aggregated Effects ------------------
coef std err t P>|t| 2.5 % 97.5 %
3.0 1.749538 0.170940 10.234790 0.000000 1.414501 2.084575
4.0 1.863187 0.189293 9.842887 0.000000 1.492180 2.234194
5.0 0.872390 0.243406 3.584099 0.000338 0.395324 1.349456
------------------ Additional Information ------------------
Score function: observational
Control group: never_treated
Anticipation periods: 0
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/doubleml/did/did_aggregation.py:368: UserWarning: Joint confidence intervals require bootstrapping which hasn't been performed yet. Automatically applying '.aggregated_frameworks.bootstrap(method="normal", n_rep_boot=500)' with default values. For different bootstrap settings, call bootstrap() explicitly before plotting.
warnings.warn(
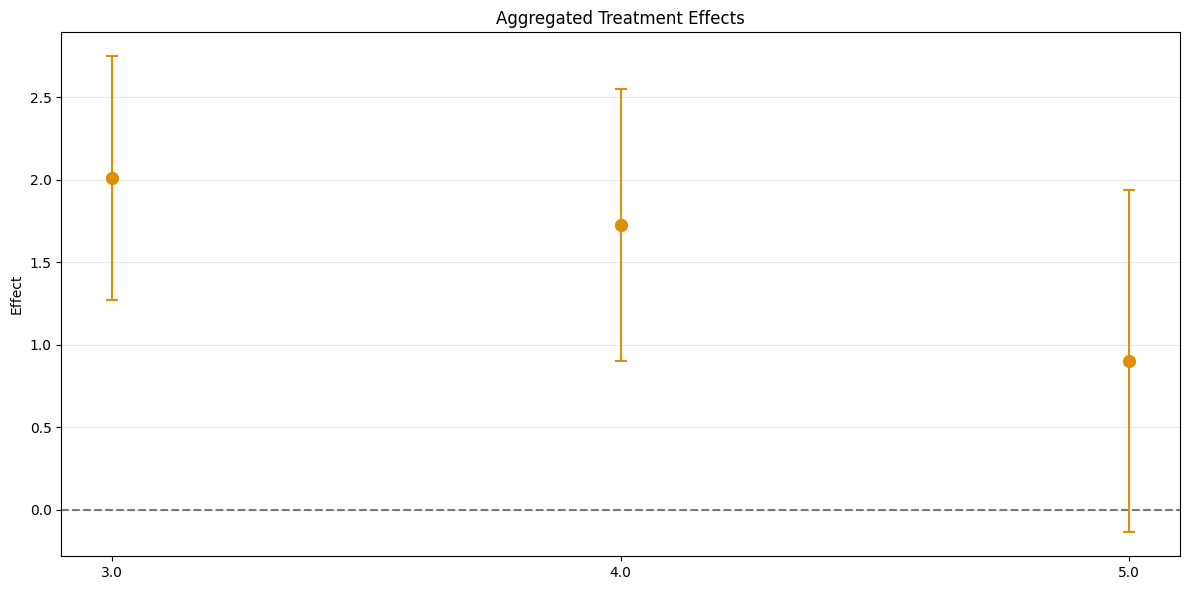
The output is a DoubleMLDIDAggregation object which includes an overall aggregation summary based on group size.
Time Aggregation#
To obtain time-specific effects one can would like to average \(ATT(\mathrm{g}, t_\text{eval})\) over \(\mathrm{g}\) (respecting group size). As a sample oracle we will combine all ite’s based on group \(\mathrm{g}\). As oracle values, we obtain
[20]:
df_post_treatment.groupby("t")["ite"].mean()
[20]:
t
3 0.969044
4 1.462502
5 1.967719
Name: ite, dtype: float64
To aggregate \(\widehat{ATT}(\mathrm{g},t_\text{pre},t_\text{eval})\), based on \(t_\text{eval}\), but weighted with respect to group size. Corresponds to Calendar Time Effects from the did-R-package.
For calendar time effects set aggregation="time".
[21]:
aggregated_time = dml_obj.aggregate("time")
print(aggregated_time)
fig, ax = aggregated_time.plot_effects()
================== DoubleMLDIDAggregation Object ==================
Time Aggregation
------------------ Overall Aggregated Effects ------------------
coef std err t P>|t| 2.5 % 97.5 %
1.436153 0.118615 12.107735 0.0 1.203673 1.668634
------------------ Aggregated Effects ------------------
coef std err t P>|t| 2.5 % 97.5 %
3 0.674924 0.220866 3.055802 2.244593e-03 0.242034 1.107815
4 1.676479 0.210565 7.961801 1.776357e-15 1.263779 2.089179
5 1.957057 0.179302 10.914858 0.000000e+00 1.605631 2.308483
------------------ Additional Information ------------------
Score function: observational
Control group: never_treated
Anticipation periods: 0
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/doubleml/did/did_aggregation.py:368: UserWarning: Joint confidence intervals require bootstrapping which hasn't been performed yet. Automatically applying '.aggregated_frameworks.bootstrap(method="normal", n_rep_boot=500)' with default values. For different bootstrap settings, call bootstrap() explicitly before plotting.
warnings.warn(
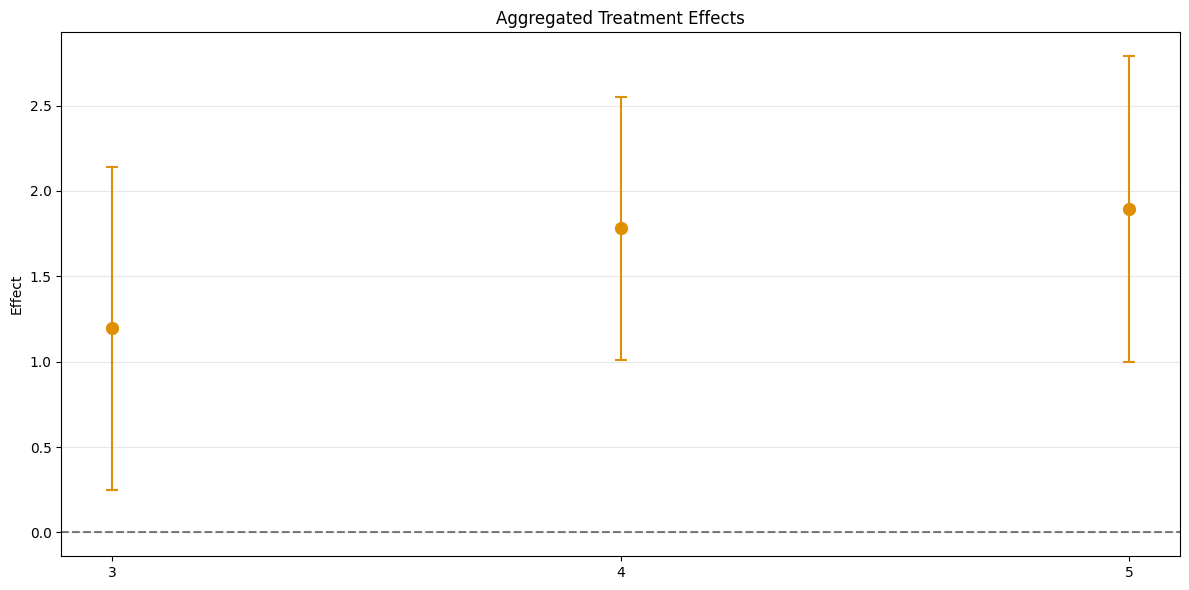
Event Study Aggregation#
To obtain event-study-type effects one can would like to aggregate \(ATT(\mathrm{g}, t_\text{eval})\) over \(e = t_\text{eval} - \mathrm{g}\) (respecting group size). As a sample oracle we will combine all ite’s based on group \(\mathrm{g}\). As oracle values, we obtain
[22]:
df_treated = df[df["d"] != np.inf].copy()
df_treated["e"] = df_treated["t"] - df_treated["d"]
df_treated.groupby("e")["ite"].mean().iloc[1:]
[22]:
e
-4.0 -0.038996
-3.0 0.011284
-2.0 -0.020027
-1.0 -0.004390
0.0 0.967693
1.0 1.957239
2.0 2.907084
Name: ite, dtype: float64
Analogously, aggregation="eventstudy" aggregates \(\widehat{ATT}(\mathrm{g},t_\text{pre},t_\text{eval})\) based on exposure time \(e = t_\text{eval} - \mathrm{g}\) (respecting group size).
[23]:
aggregated_eventstudy = dml_obj.aggregate("eventstudy")
print(aggregated_eventstudy)
aggregated_eventstudy.plot_effects()
================== DoubleMLDIDAggregation Object ==================
Event Study Aggregation
------------------ Overall Aggregated Effects ------------------
coef std err t P>|t| 2.5 % 97.5 %
1.920088 0.13878 13.835434 0.0 1.648083 2.192092
------------------ Aggregated Effects ------------------
coef std err t P>|t| 2.5 % 97.5 %
-4.0 -0.019087 0.093422 -0.204308 0.838113 -0.202191 0.164017
-3.0 -0.010619 0.070186 -0.151296 0.879742 -0.148180 0.126942
-2.0 -0.131891 0.064998 -2.029140 0.042444 -0.259285 -0.004496
-1.0 0.076256 0.085593 0.890917 0.372974 -0.091503 0.244015
0.0 0.999730 0.108777 9.190675 0.000000 0.786532 1.212928
1.0 2.054432 0.185120 11.097869 0.000000 1.691604 2.417259
2.0 2.706101 0.247841 10.918707 0.000000 2.220342 3.191860
------------------ Additional Information ------------------
Score function: observational
Control group: never_treated
Anticipation periods: 0
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/doubleml/did/did_aggregation.py:368: UserWarning: Joint confidence intervals require bootstrapping which hasn't been performed yet. Automatically applying '.aggregated_frameworks.bootstrap(method="normal", n_rep_boot=500)' with default values. For different bootstrap settings, call bootstrap() explicitly before plotting.
warnings.warn(
[23]:
(<Figure size 1200x600 with 1 Axes>,
<Axes: title={'center': 'Aggregated Treatment Effects'}, ylabel='Effect'>)
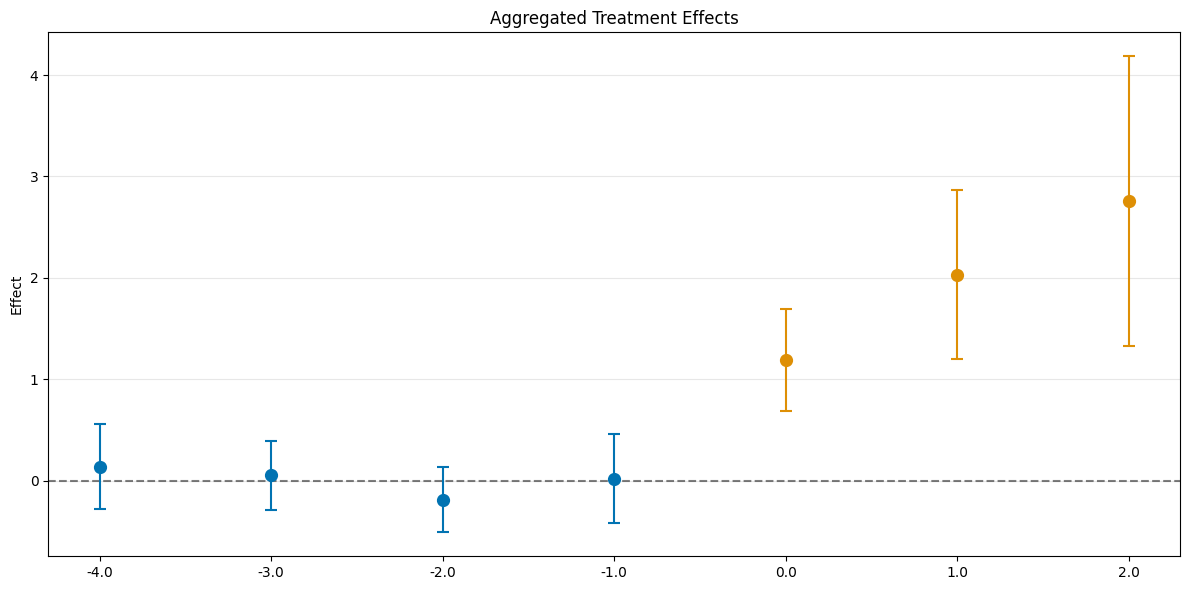
Aggregation Details#
The DoubleMLDIDAggregation objects include several DoubleMLFrameworks which support methods like bootstrap() or confint(). Further, the weights can be accessed via the properties
overall_aggregation_weights: weights for the overall aggregationaggregation_weights: weights for the aggregation
To clarify, e.g. for the eventstudy aggregation
[24]:
print(aggregated_eventstudy)
================== DoubleMLDIDAggregation Object ==================
Event Study Aggregation
------------------ Overall Aggregated Effects ------------------
coef std err t P>|t| 2.5 % 97.5 %
1.920088 0.13878 13.835434 0.0 1.648083 2.192092
------------------ Aggregated Effects ------------------
coef std err t P>|t| 2.5 % 97.5 %
-4.0 -0.019087 0.093422 -0.204308 0.838113 -0.202191 0.164017
-3.0 -0.010619 0.070186 -0.151296 0.879742 -0.148180 0.126942
-2.0 -0.131891 0.064998 -2.029140 0.042444 -0.259285 -0.004496
-1.0 0.076256 0.085593 0.890917 0.372974 -0.091503 0.244015
0.0 0.999730 0.108777 9.190675 0.000000 0.786532 1.212928
1.0 2.054432 0.185120 11.097869 0.000000 1.691604 2.417259
2.0 2.706101 0.247841 10.918707 0.000000 2.220342 3.191860
------------------ Additional Information ------------------
Score function: observational
Control group: never_treated
Anticipation periods: 0
Here, the overall effect aggregation aggregates each effect with positive exposure
[25]:
print(aggregated_eventstudy.overall_aggregation_weights)
[0. 0. 0. 0. 0.33333333 0.33333333
0.33333333]
If one would like to consider how the aggregated effect with \(e=0\) is computed, one would have to look at the corresponding set of weights within the aggregation_weights property
[26]:
# the weights for e=0 correspond to the fifth element of the aggregation weights
aggregated_eventstudy.aggregation_weights[4]
[26]:
array([0. , 0. , 0.34627716, 0. , 0. ,
0. , 0. , 0. , 0.3257036 , 0. ,
0. , 0. , 0. , 0. , 0.32801924])
Taking a look at the original dml_obj, one can see that this combines the following estimates (only show month):
\(\widehat{ATT}(04,03,04)\)
\(\widehat{ATT}(05,04,05)\)
\(\widehat{ATT}(06,05,06)\)
[27]:
print(dml_obj.summary["coef"])
ATT(3.0,0,1) -0.234497
ATT(3.0,1,2) 0.276271
ATT(3.0,2,3) 0.674924
ATT(3.0,2,4) 1.867589
ATT(3.0,2,5) 2.706101
ATT(4.0,0,1) -0.107650
ATT(4.0,1,2) 0.088173
ATT(4.0,2,3) -0.336062
ATT(4.0,3,4) 1.473297
ATT(4.0,3,5) 2.253077
ATT(5.0,0,1) -0.019087
ATT(5.0,1,2) 0.085728
ATT(5.0,2,3) -0.242083
ATT(5.0,3,4) 0.274516
ATT(5.0,4,5) 0.872390
Name: coef, dtype: float64
Anticipation#
As described in the Model Guide, one can include anticipation periods \(\delta>0\) by setting the anticipation_periods parameter.
Data with Anticipation#
The DGP allows to include anticipation periods via the anticipation_periods parameter. In this case the observations will be “shifted” such that units anticipate the effect earlier and the exposure effect is increased by the number of periods where the effect is anticipated.
[28]:
n_obs = 4000
n_periods = 6
df_anticipation = make_did_cs_CS2021(n_obs, dgp_type=4, n_periods=n_periods, n_pre_treat_periods=3, time_type="datetime", anticipation_periods=1)
print(df_anticipation.shape)
df_anticipation.head()
(19437, 10)
[28]:
| id | y | y0 | y1 | d | t | Z1 | Z2 | Z3 | Z4 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 209.457547 | 209.457547 | 207.495586 | 2025-06-01 | 2025-01-01 | -0.035860 | -0.448609 | -0.198811 | -0.117202 |
| 4 | 0 | 209.386566 | 209.386566 | 209.747526 | 2025-06-01 | 2025-04-01 | -0.035860 | -0.448609 | -0.198811 | -0.117202 |
| 5 | 0 | 211.772281 | 210.223770 | 211.772281 | 2025-06-01 | 2025-05-01 | -0.035860 | -0.448609 | -0.198811 | -0.117202 |
| 6 | 0 | 210.541602 | 211.186482 | 210.541602 | 2025-06-01 | 2025-06-01 | -0.035860 | -0.448609 | -0.198811 | -0.117202 |
| 9 | 1 | 227.996057 | 227.996057 | 228.254338 | 2025-05-01 | 2025-02-01 | 0.665015 | 0.740742 | -0.283006 | 0.921473 |
To visualize the anticipation, we will again plot the “oracle” values
[29]:
df_anticipation["ite"] = df_anticipation["y1"] - df_anticipation["y0"]
agg_df_anticipation = df_anticipation.groupby(["t", "d"]).agg(**agg_dictionary).reset_index()
agg_df_anticipation.head()
[29]:
| t | d | y_mean | y_lower_quantile | y_upper_quantile | ite_mean | ite_lower_quantile | ite_upper_quantile | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2025-01-01 | 2025-04-01 | 208.258305 | 191.804950 | 224.460365 | -0.039019 | -2.266961 | 2.449498 |
| 1 | 2025-01-01 | 2025-05-01 | 210.852652 | 194.149637 | 228.115662 | 0.054900 | -2.294053 | 2.324122 |
| 2 | 2025-01-01 | 2025-06-01 | 213.468017 | 196.482378 | 229.990592 | -0.082219 | -2.425386 | 2.262948 |
| 3 | 2025-02-01 | 2025-04-01 | 208.625625 | 184.348145 | 233.590775 | -0.001922 | -2.390319 | 2.198127 |
| 4 | 2025-02-01 | 2025-05-01 | 211.422667 | 185.505941 | 236.139765 | -0.017127 | -2.408349 | 2.315649 |
One can see that the effect is already anticipated one period before the actual treatment assignment.
[30]:
plot_data(agg_df_anticipation, col_name='ite')
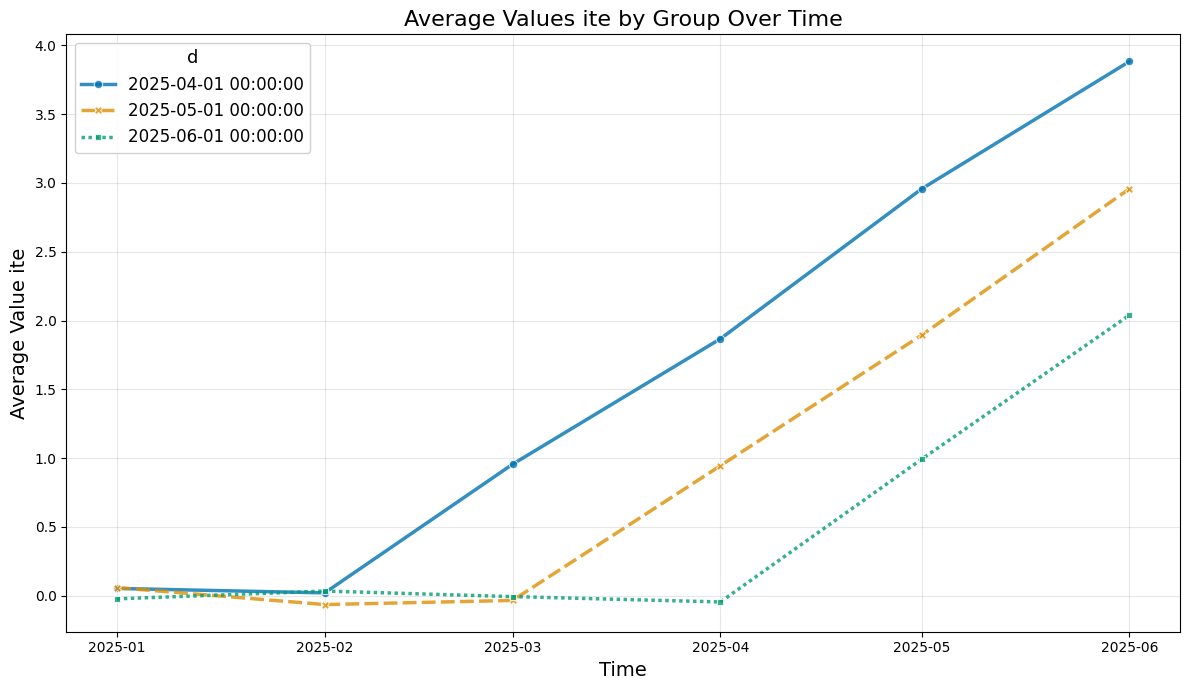
Initialize a corresponding DoubleMLPanelData object.
[31]:
dml_data_anticipation = DoubleMLPanelData(
data=df_anticipation,
y_col="y",
d_cols="d",
id_col="id",
t_col="t",
x_cols=["Z1", "Z2", "Z3", "Z4"],
datetime_unit="M"
)
ATT Estimation#
Let us take a look at the estimation without anticipation.
[32]:
dml_obj_anticipation = DoubleMLDIDMulti(dml_data_anticipation, **default_args)
dml_obj_anticipation.fit()
dml_obj_anticipation.bootstrap(n_rep_boot=5000)
dml_obj_anticipation.plot_effects()
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
[32]:
(<Figure size 1200x800 with 4 Axes>,
[<Axes: title={'center': 'First Treated: 2025-04'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 2025-05'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 2025-06'}, xlabel='Evaluation Period', ylabel='Effect'>])
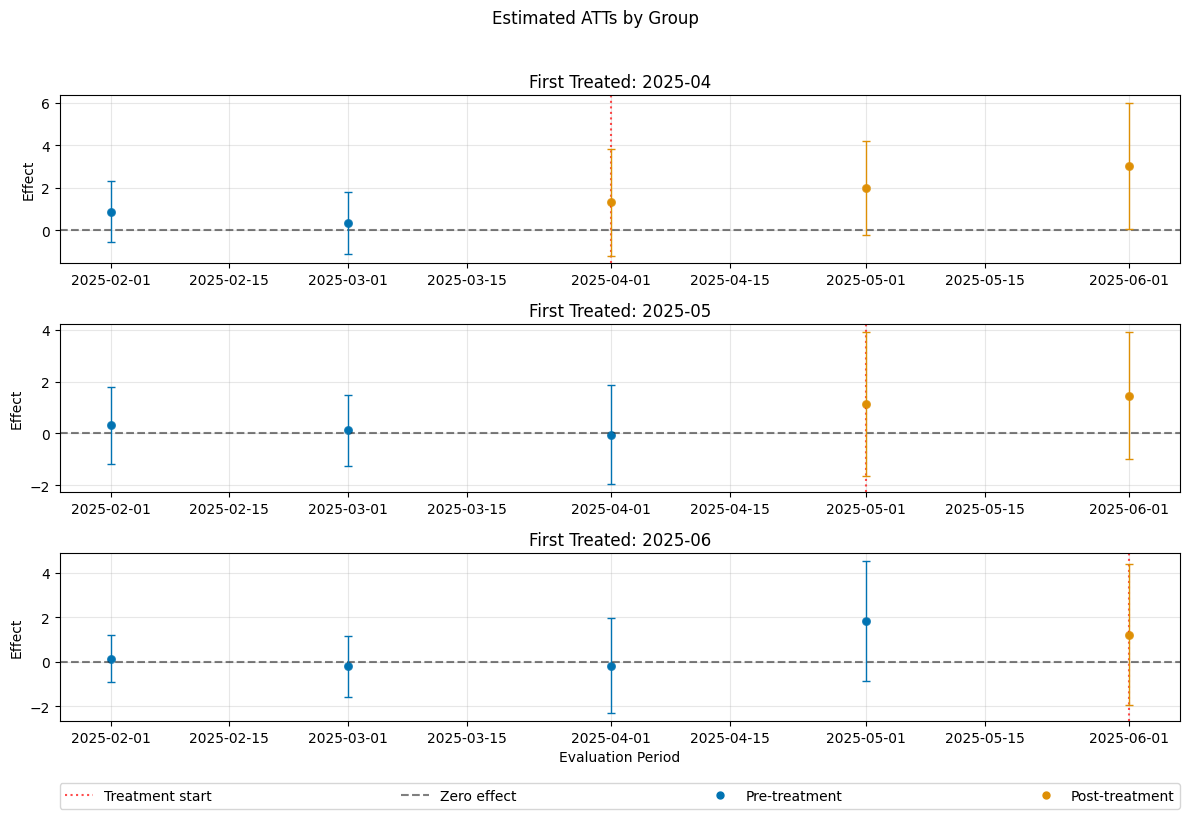
The effects are obviously biased. To include anticipation periods, one can adjust the anticipation_periods parameter. Correspondingly, the outcome regression (and not yet treated units) are adjusted.
[33]:
dml_obj_anticipation = DoubleMLDIDMulti(dml_data_anticipation, **(default_args| {"anticipation_periods": 1}))
dml_obj_anticipation.fit()
dml_obj_anticipation.bootstrap(n_rep_boot=5000)
dml_obj_anticipation.plot_effects()
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
[33]:
(<Figure size 1200x800 with 4 Axes>,
[<Axes: title={'center': 'First Treated: 2025-04'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 2025-05'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 2025-06'}, xlabel='Evaluation Period', ylabel='Effect'>])
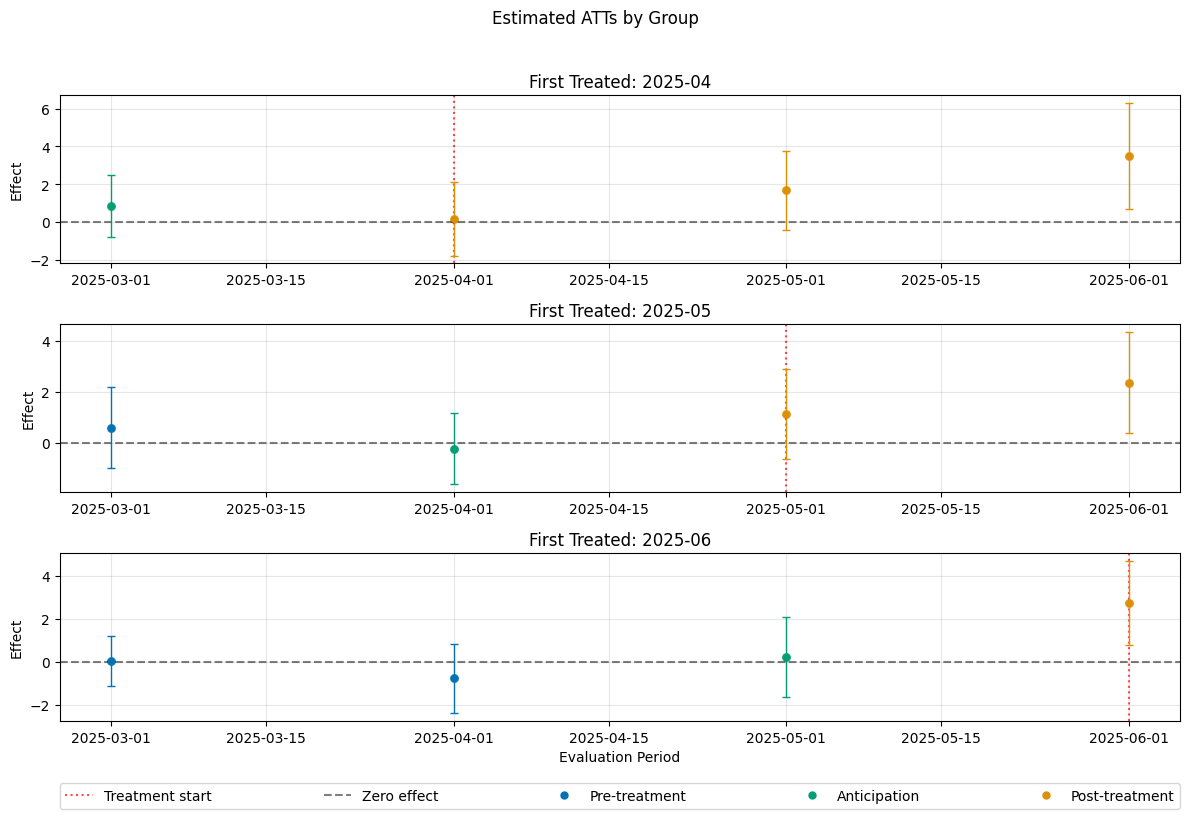
Group-Time Combinations#
The default option gt_combinations="standard" includes all group time values with the specific choice of \(t_\text{pre} = \min(\mathrm{g}, t_\text{eval}) - 1\) (without anticipation) which is the weakest possible parallel trend assumption.
Other options are possible or only specific combinations of \((\mathrm{g},t_\text{pre},t_\text{eval})\).
All combinations#
The option gt_combinations="all" includes all relevant group time values with \(t_\text{pre} < \min(\mathrm{g}, t_\text{eval})\), including longer parallel trend assumptions. This can result in multiple estimates for the same \(ATT(\mathrm{g},t)\), which have slightly different assumptions (length of parallel trends).
[34]:
dml_obj_all = DoubleMLDIDMulti(dml_data, **(default_args| {"gt_combinations": "all"}))
dml_obj_all.fit()
dml_obj_all.bootstrap(n_rep_boot=5000)
dml_obj_all.plot_effects()
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
[34]:
(<Figure size 1200x800 with 4 Axes>,
[<Axes: title={'center': 'First Treated: 3.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 4.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 5.0'}, xlabel='Evaluation Period', ylabel='Effect'>])
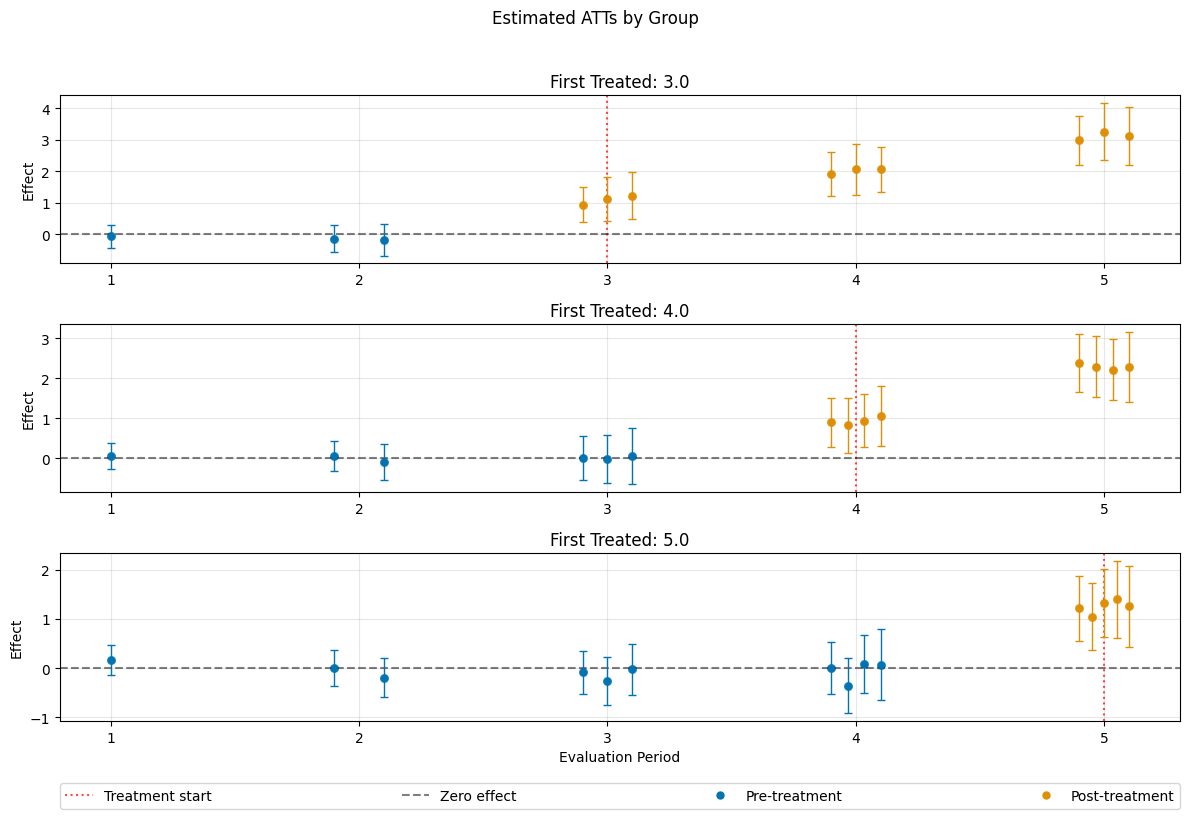
Universal Base Period#
The option gt_combinations="universal" set \(t_\text{pre} = \mathrm{g} - \delta - 1\), corresponding to a universal/constant comparison or base period.
Remark that this implies \(t_\text{pre} > t_\text{eval}\) for all pre-treatment periods (accounting for anticipation). Therefore these effects do not have the same straightforward interpretation as ATT’s.
[35]:
dml_obj_universal = DoubleMLDIDMulti(dml_data, **(default_args| {"gt_combinations": "universal"}))
dml_obj_universal.fit()
dml_obj_universal.bootstrap(n_rep_boot=5000)
dml_obj_universal.plot_effects()
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/matplotlib/cbook.py:1719: FutureWarning: Calling float on a single element Series is deprecated and will raise a TypeError in the future. Use float(ser.iloc[0]) instead
return math.isfinite(val)
[35]:
(<Figure size 1200x800 with 4 Axes>,
[<Axes: title={'center': 'First Treated: 3.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 4.0'}, ylabel='Effect'>,
<Axes: title={'center': 'First Treated: 5.0'}, xlabel='Evaluation Period', ylabel='Effect'>])
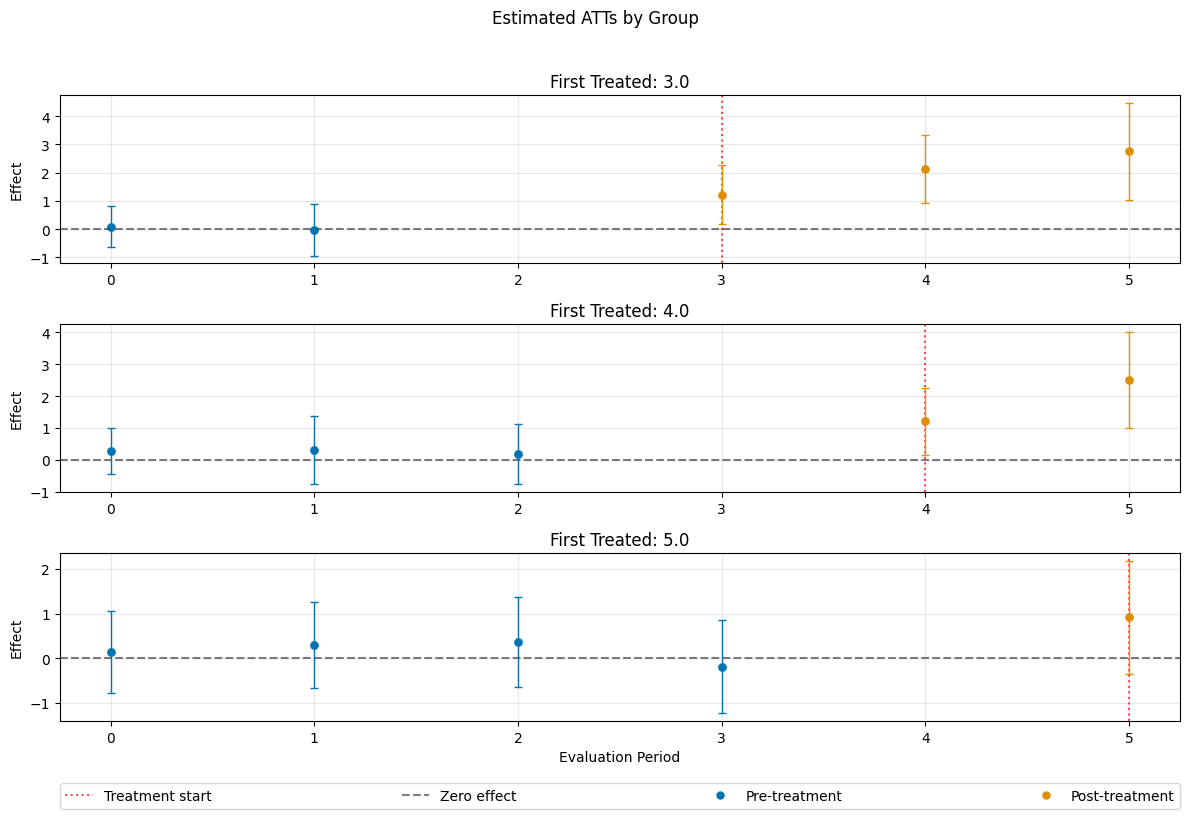
Selected Combinations#
Instead it is also possible to just submit a list of tuples containing \((\mathrm{g}, t_\text{pre}, t_\text{eval})\) combinations. E.g. only two combinations
[36]:
gt_dict = {
"gt_combinations": [
(4.0, 1, 2),
(4.0, 1, 3),
]
}
dml_obj_all = DoubleMLDIDMulti(dml_data, **(default_args| gt_dict))
dml_obj_all.fit()
dml_obj_all.bootstrap(n_rep_boot=5000)
dml_obj_all.plot_effects()
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMRegressor was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but LGBMClassifier was fitted with feature names
warnings.warn(
[36]:
(<Figure size 1200x800 with 2 Axes>,
[<Axes: title={'center': 'First Treated: 4.0'}, xlabel='Evaluation Period', ylabel='Effect'>])