Note
-
Download Jupyter notebook:
https://docs.doubleml.org/stable/examples/py_double_ml_rdflex.ipynb.
Flexible Covariate Adjustment in Regression Discontinuity Designs (RDD)#
This notebook demonstrates how to use RDD within DoubleML. Our implementation, RDFlex, is based on the paper “Flexible Covariate Adjustments in Regression Discontinuity Designs” by Noack, Olma and Rothe (2024).
In regression discontinuity designs (RDD), treatment assignment is determined by a continuous running variable \(S\) (or “score”) crossing a known threshold \(c\) (or “cutoff”). We aim to estimate the average treatment effect locally at the cutoff,
with \(Y_i(1)\) and \(Y_i(0)\) denoting the potential outcomes of an individual with and without treatment, respectively.
Note: The dependencies for the module doubleml.rdd can be installed seperately via pip install rdrobust, if necessary.
[1]:
import numpy as np
import pandas as pd
import plotly.express as px
import plotly.graph_objs as go
from statsmodels.nonparametric.kernel_regression import KernelReg
from lightgbm import LGBMRegressor, LGBMClassifier
from rdrobust import rdrobust
import doubleml as dml
from doubleml.rdd import RDFlex
from doubleml.rdd.datasets import make_simple_rdd_data
Sharp RDD#
In the sharp design, the treatment assignment is deterministic given the score. Namely, all the individuals with a score higher than the cutoff, receive the treatment
Without loss of generality, for the whole example we consider the cutoff to be normalized to \(c=0\) and formulas are given accordingly.
In sharp RDD, the treatment effect defined above is identified by
A key assumption for this identification is the continuity of the conditional expectations of the potential outcomes \(\mathbb{E}[Y_i(d)\mid S_i=c]\) for \(d \in \{0, 1\}\).
This implies that units cannot perfectly manipulate their score to either receive or avoid treatment exactly at the cutoff.
Generate Sharp Data#
The function make_simple_rdd_data() can be used to generate data of a rather standard RDD setting. If we set fuzzy = False, the generated data follows a sharp RDD. We also generate covariates \(X\) that can be used to adjust the estimation at a later stage. By default, the cutoff is normalized to c = 0. The true RDD effect can be controlled by tau and is set to a value of \(2.0\) in this example.
[2]:
np.random.seed(1234)
true_tau = 2.0
data_dict = make_simple_rdd_data(n_obs=1000, fuzzy=False, tau=true_tau)
cov_names = ['x' + str(i) for i in range(data_dict['X'].shape[1])]
df = pd.DataFrame(
np.column_stack((data_dict['Y'], data_dict['D'], data_dict['score'], data_dict['X'])),
columns=['y', 'd', 'score'] + cov_names,
)
df.head()
[2]:
| y | d | score | x0 | x1 | x2 | |
|---|---|---|---|---|---|---|
| 0 | 1.563067 | 1.0 | 0.471435 | -0.198503 | -0.193849 | -0.493426 |
| 1 | 1.348622 | 0.0 | -1.190976 | 0.013677 | -0.630880 | -0.885832 |
| 2 | 2.265929 | 1.0 | 1.432707 | -0.266147 | 0.439675 | -0.051651 |
| 3 | 7.477357 | 0.0 | -0.312652 | 0.845241 | -0.659755 | 0.436764 |
| 4 | 13.185130 | 0.0 | -0.720589 | 0.739595 | -0.741380 | 0.948112 |
Comparing the observed outcomes, we can clearly see a discontinuity at the cutoff value of \(c = 0\).
[3]:
fig = px.scatter(
x=df['score'],
y=df['y'],
color=df['d'].astype(bool),
labels={
"x": "Score",
"y": "Outcome",
"color": "Treatment"
},
title="Scatter Plot of Outcome vs. Score by Treatment Status"
)
fig.update_layout(
xaxis_title="Score",
yaxis_title="Outcome"
)
fig.show()
Sharp RDD Without Adjustment#
The standard RDD estimator for the sharp design takes the form
where the \(w_i(h)\) are local linear regression weights that depend on the data through the realizations of the running variable only and \(h > 0\) is a bandwidth.
The packages rdrobust implements this estimation.
[4]:
rdrobust_sharp_noadj = rdrobust(y=df['y'], x=df['score'], fuzzy=df['d'], c=0.0)
rdrobust_sharp_noadj
Call: rdrobust
Number of Observations: 1000
Polynomial Order Est. (p): 1
Polynomial Order Bias (q): 2
Kernel: Triangular
Bandwidth Selection: mserd
Var-Cov Estimator: NN
Left Right
------------------------------------------------
Number of Observations 493 507
Number of Unique Obs. 493 507
Number of Effective Obs. 291 299
Bandwidth Estimation 0.78 0.78
Bandwidth Bias 1.282 1.282
rho (h/b) 0.608 0.608
Method Coef. S.E. t-stat P>|t| 95% CI
-------------------------------------------------------------------------
Conventional 2.407 0.634 3.795 1.475e-04 [1.164, 3.65]
Robust - - 3.122 1.796e-03 [0.869, 3.802]
[4]:
Sharp RDD with Linear Adjustment#
The linearly adjusted RDD estimator for the sharp design takes the form
where \(w_i(h)\) are local linear regression weights that depend on the data through the realizations of the running variable \(S_i\) only and \(h>0\) is a bandwidth. \(\hat{\gamma}_h\) is a minimizer from the regression
with \(Q_i =(D_i, S_i, D_i S_i,1)^T\) (for more details, see our User Guide), \(K_h(v)=K(v/h)/h\) with \(K(\cdot)\) a kernel function.
The packages rdrobust implements this estimation with a linear adjustment.
[5]:
rdrobust_sharp = rdrobust(y=df['y'], x=df['score'], fuzzy=df['d'], covs=df[cov_names], c=0.0)
rdrobust_sharp
Call: rdrobust
Number of Observations: 1000
Polynomial Order Est. (p): 1
Polynomial Order Bias (q): 2
Kernel: Triangular
Bandwidth Selection: mserd
Var-Cov Estimator: NN
Left Right
------------------------------------------------
Number of Observations 493 507
Number of Unique Obs. 493 507
Number of Effective Obs. 281 285
Bandwidth Estimation 0.732 0.732
Bandwidth Bias 1.22 1.22
rho (h/b) 0.6 0.6
Method Coef. S.E. t-stat P>|t| 95% CI
-------------------------------------------------------------------------
Conventional 2.207 0.433 5.099 3.416e-07 [1.359, 3.056]
Robust - - 4.311 1.629e-05 [1.189, 3.172]
[5]:
Sharp RDD with Flexible Adjustment#
Noack, Olma and Rothe (2024) propose an estimator that reduces the variance of the above esimator, using a flexible adjustment of the outcome by machine learning. For more details, see our User Guide. The estimator here takes the form
with \(\eta(\cdot)\) being potentially nonlinear adjustment functions.
We initialize a DoubleMLData object using the usual package syntax:
y_colrefers to the observed outcome, on which we want to estimate the effect at the cutoffs_colrefers to the scorex_colsrefers to the covariates to be adjusted ford_colsis an indicator whether an observation is treated or not. In the sharp design, this should be identical to an indicator whether an observation is left or right of the cutoff (\(D_i = \mathbb{I}[S_i \geq c]\))
[6]:
dml_data_sharp = dml.DoubleMLRDDData(df, y_col='y', d_cols='d', x_cols=cov_names, score_col='score')
The RDFlex object is intialized with only one learner, that adjusts the outcome based on the covariates.
[7]:
ml_g = LGBMRegressor(n_estimators=500, learning_rate=0.01, verbose=-1)
rdflex_sharp = RDFlex(dml_data_sharp,
ml_g,
cutoff=0,
fuzzy=False,
n_folds=5,
n_rep=1)
rdflex_sharp.fit(n_iterations=2)
print(rdflex_sharp)
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
Method Coef. S.E. t-stat P>|t| 95% CI
-------------------------------------------------------------------------
Conventional 2.014 0.103 19.494 1.231e-84 [1.812, 2.217]
Robust - - 16.872 7.173e-64 [1.779, 2.247]
Design Type: Sharp
Cutoff: 0
First Stage Kernel: triangular
Final Bandwidth: [0.6607402]
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
It is visible that the flexible adjustment decreases the standard error in the estimation and therefore provides tighter confidence intervals. For coverage simulations, see the DoubleML Coverage Repository.
RDFlex uses an iterative fitting approach to determine a preliminary bandwidth selections for the local adjustments. The default number of iterations is n_iterations=2, according to Noack, Olma and Rothe (2024).
Fuzzy RDD#
In the fuzzy RDDs, the treatment assignment is still deterministic given the score \(\left(T_i = \mathbb{I}[S_i \geq c]\right)\). However, in the neighborhood of the cutoff, there is a probability of non-compliance. Thus, the treatment received might differ from the assigned one \((D_i \neq T_i)\) for some units. These observations cause the jump in the probability of treatment at the cutoff to be smaller than 1 but larger than 0. In other words, around the cutoff there can be treatment randomization on both sides.
The parameter of interest in the Fuzzy RDD is the average treatment effect at the cutoff, for all individuals that comply with the assignment
This effect can be identified by
Generate Fuzzy Data#
The function make_simple_rdd_data() with fuzzy = True generates basic data for the fuzzy case. The cutoff is still set to \(c = 0\) and we set the true effect to be tau = 2.0 again.
[8]:
np.random.seed(1234)
data_dict = make_simple_rdd_data(n_obs=1000, fuzzy=True, tau=true_tau)
cov_names = ['x' + str(i) for i in range(data_dict['X'].shape[1])]
df = pd.DataFrame(
np.column_stack((data_dict['Y'], data_dict['D'], data_dict['score'], data_dict['X'])),
columns=['y', 'd', 'score'] + cov_names,
)
df.head()
[8]:
| y | d | score | x0 | x1 | x2 | |
|---|---|---|---|---|---|---|
| 0 | -0.183553 | 0.0 | 0.471435 | -0.198503 | -0.193849 | -0.493426 |
| 1 | 1.348622 | 0.0 | -1.190976 | 0.013677 | -0.630880 | -0.885832 |
| 2 | 2.265929 | 1.0 | 1.432707 | -0.266147 | 0.439675 | -0.051651 |
| 3 | 9.694561 | 1.0 | -0.312652 | 0.845241 | -0.659755 | 0.436764 |
| 4 | 15.001403 | 1.0 | -0.720589 | 0.739595 | -0.741380 | 0.948112 |
Comparing the observed outcomes, the discontinuity is less pronounced than in the sharp case. We see some degree of randomization left and right of the cutoff.
[9]:
fig = px.scatter(
x=df['score'],
y=df['y'],
color=df['d'].astype(bool),
labels={
"x": "Score",
"y": "Outcome",
"color": "Treatment"
},
title="Scatter Plot of Outcome vs. Score by Treatment Status"
)
fig.update_layout(
xaxis_title="Score",
yaxis_title="Outcome"
)
fig.show()
Fuzzy RDD Without Adjustment#
The standard RDD estimator for the fuzzy design takes the form
The packages rdrobust implements this estimation.
[10]:
rdrobust_fuzzy_noadj = rdrobust(y=df['y'], x=df['score'], fuzzy=df['d'], c=0.0)
rdrobust_fuzzy_noadj
Call: rdrobust
Number of Observations: 1000
Polynomial Order Est. (p): 1
Polynomial Order Bias (q): 2
Kernel: Triangular
Bandwidth Selection: mserd
Var-Cov Estimator: NN
Left Right
------------------------------------------------
Number of Observations 493 507
Number of Unique Obs. 493 507
Number of Effective Obs. 213 224
Bandwidth Estimation 0.542 0.542
Bandwidth Bias 0.864 0.864
rho (h/b) 0.628 0.628
Method Coef. S.E. t-stat P>|t| 95% CI
-------------------------------------------------------------------------
Conventional 4.64 3.052 1.52 1.285e-01 [-1.343, 10.622]
Robust - - 1.414 1.575e-01 [-1.952, 12.054]
[10]:
Fuzzy RDD with Linear Adjustment#
The linearly adjusted RDD estimator for the fuzzy design takes the form
Under similar assumptions as in the sharp case and that there are no Defiers (= individuals that would always pick the opposite treatment of their assigned one), this effect estimates the average treatment effect at the cutoff. The package rdrobust implements this estimation with a linear adjustment.
[11]:
rdrobust_fuzzy = rdrobust(y=df['y'], x=df['score'], fuzzy=df['d'], covs=df[cov_names], c=0.0)
rdrobust_fuzzy
Call: rdrobust
Number of Observations: 1000
Polynomial Order Est. (p): 1
Polynomial Order Bias (q): 2
Kernel: Triangular
Bandwidth Selection: mserd
Var-Cov Estimator: NN
Left Right
------------------------------------------------
Number of Observations 493 507
Number of Unique Obs. 493 507
Number of Effective Obs. 211 223
Bandwidth Estimation 0.54 0.54
Bandwidth Bias 0.88 0.88
rho (h/b) 0.614 0.614
Method Coef. S.E. t-stat P>|t| 95% CI
-------------------------------------------------------------------------
Conventional 2.802 2.326 1.205 2.283e-01 [-1.757, 7.361]
Robust - - 1.097 2.728e-01 [-2.367, 8.381]
[11]:
The fuzzy design usually has much larger standard errors than the sharp design, as the jump in treatment probability adds further estimation uncertainty.
Fuzzy RDD with Flexible Adjustment#
Noack, Olma and Rothe (2024) propose an estimator that reduces the variance of the above esimator, using a flexible adjustment of the outcome by ML. For more details, see our User Guide. The estimator here takes the form
with \(\eta_Y(\cdot), \eta_D(\cdot)\) being potentially nonlinear adjustment functions.
We initialize a DoubleMLData object using the usual package syntax:
y_colrefers to the observed outcome, on which we want to estimate the effect at the cutoffs_colrefers to the scorex_colsrefers to the covariates to be adjusted ford_colsis an indicator whether an observation is treated or not. In the fuzzy design, this should not be identical to an indicator whether an observation is left or right of the cutoff (\(D_i \neq \mathbb{I}[S_i \geq c]\))
[12]:
dml_data_fuzzy = dml.DoubleMLRDDData(df, y_col='y', d_cols='d', x_cols=cov_names, score_col='score')
This time, we also have to specify a classifier that adjusts the treatment assignment probabilities.
[13]:
ml_g = LGBMRegressor(n_estimators=500, learning_rate=0.01, verbose=-1)
ml_m = LGBMClassifier(n_estimators=500, learning_rate=0.01, verbose=-1)
rdflex_fuzzy = RDFlex(dml_data_fuzzy,
ml_g,
ml_m,
cutoff=0,
fuzzy=True,
n_folds=5,
n_rep=1)
rdflex_fuzzy.fit(n_iterations=2)
print(rdflex_fuzzy)
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMRegressor was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
Method Coef. S.E. t-stat P>|t| 95% CI
-------------------------------------------------------------------------
Conventional 0.979 0.726 1.348 1.777e-01 [-0.445, 2.403]
Robust - - 0.994 3.201e-01 [-0.831, 2.541]
Design Type: Fuzzy
Cutoff: 0
First Stage Kernel: triangular
Final Bandwidth: [0.61170069]
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
/home/ubuntu/.venv/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning:
X does not have valid feature names, but LGBMClassifier was fitted with feature names
Also for the fuzzy case, we observe a significant decrease in estimation standard error.
Advanced: Global and Local Learners, Stacked Ensembles#
By default, RDFlex fits ML methods using kernel weights, resulting in a “local” fit around the cutoff. If the adjustment should also include “global” information from the full support of \(S\) available in the data, the use of a the GlobalLearner wrapper is recommended.
The GlobalLearner allows to ignore the weights and fit the ML method on the full support of the data, even if weights are provided.
The learners can also be stacked. All learners have to support the sample_weight in their fit method. By stacking and using local and global learners, it is possible to further tune the estimation and potentially reduce standard errors even further.
[14]:
from doubleml.utils import GlobalRegressor, GlobalClassifier
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
from sklearn.ensemble import StackingClassifier, StackingRegressor
[15]:
reg_estimators = [
('lr local', LinearRegression()),
('rf local', RandomForestRegressor()),
('lr global', GlobalRegressor(base_estimator=LinearRegression())),
('rf global', GlobalRegressor(base_estimator=RandomForestRegressor()))
]
class_estimators = [
('lr local', LogisticRegression()),
('rf local', RandomForestClassifier()),
('lr global', GlobalClassifier(base_estimator=LogisticRegression())),
('rf global', GlobalClassifier(base_estimator=RandomForestClassifier()))
]
ml_g = StackingRegressor(
estimators=reg_estimators,
final_estimator=LinearRegression(),
)
ml_m = StackingClassifier(
estimators=class_estimators,
final_estimator=LogisticRegression(),
)
We first repeat the estimation of the sharp design and observe an even smaller standard error.
[16]:
rdflex_sharp_stack = RDFlex(dml_data_sharp,
ml_g,
fuzzy=False,
n_folds=5,
n_rep=1)
rdflex_sharp_stack.fit(n_iterations=2)
print(rdflex_sharp_stack)
Method Coef. S.E. t-stat P>|t| 95% CI
-------------------------------------------------------------------------
Conventional 1.876 0.101 18.619 2.241e-77 [1.678, 2.073]
Robust - - 15.992 1.443e-57 [1.612, 2.062]
Design Type: Sharp
Cutoff: 0
First Stage Kernel: triangular
Final Bandwidth: [0.61771229]
The same applies for the fuzzy case.
[17]:
rdflex_fuzzy_stack = RDFlex(dml_data_fuzzy,
ml_g,
ml_m,
fuzzy=True,
n_folds=5,
n_rep=1)
rdflex_fuzzy_stack.fit(n_iterations=2)
print(rdflex_fuzzy_stack)
Method Coef. S.E. t-stat P>|t| 95% CI
-------------------------------------------------------------------------
Conventional 1.726 0.609 2.835 4.577e-03 [0.533, 2.918]
Robust - - 2.642 8.243e-03 [0.483, 3.261]
Design Type: Fuzzy
Cutoff: 0
First Stage Kernel: triangular
Final Bandwidth: [0.54550506]
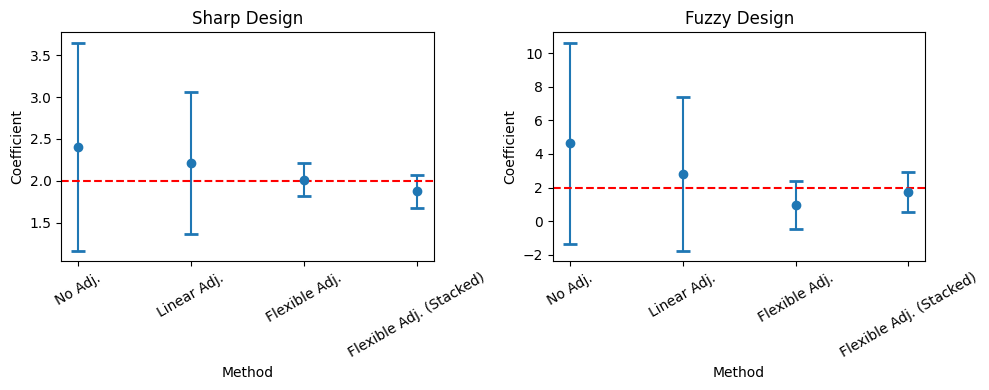
To conclude, we look at a visualization of the estimated coefficient and the confidence intervals. We see that by using the flexible adjustment, it is possible to shrink confidence intervals.
[18]:
df_sharp = pd.DataFrame({"coef": [rdrobust_sharp_noadj.coef.values[0][0], rdrobust_sharp.coef.values[0][0], rdflex_sharp.coef[0], rdflex_sharp_stack.coef[0]],
"CI lower": [rdrobust_sharp_noadj.ci.values[0][0], rdrobust_sharp.ci.values[0][0], rdflex_sharp.confint().values[0][0], rdflex_sharp_stack.confint().values[0][0]],
"CI upper": [rdrobust_sharp_noadj.ci.values[0][1], rdrobust_sharp.ci.values[0][1], rdflex_sharp.confint().values[0][1], rdflex_sharp_stack.confint().values[0][1]],
"method": ["No Adj.", "Linear Adj.", "Flexible Adj.", "Flexible Adj. (Stacked)"]})
df_fuzzy = pd.DataFrame({"coef": [rdrobust_fuzzy_noadj.coef.values[0][0], rdrobust_fuzzy.coef.values[0][0], rdflex_fuzzy.coef[0], rdflex_fuzzy_stack.coef[0]],
"CI lower": [rdrobust_fuzzy_noadj.ci.values[0][0], rdrobust_fuzzy.ci.values[0][0], rdflex_fuzzy.confint().values[0][0], rdflex_fuzzy_stack.confint().values[0][0]],
"CI upper": [rdrobust_fuzzy_noadj.ci.values[0][1], rdrobust_fuzzy.ci.values[0][1], rdflex_fuzzy.confint().values[0][1], rdflex_fuzzy_stack.confint().values[0][1]],
"method": ["No Adj.", "Linear Adj.", "Flexible Adj.", "Flexible Adj. (Stacked)"]})
[19]:
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
axes[0].errorbar(
df_sharp['method'],
df_sharp['coef'],
yerr=(df_sharp['coef'] - df_sharp['CI lower'], df_sharp['CI upper'] - df_sharp['coef']),
fmt='o',
capsize=5,
capthick=2
)
axes[0].set_title('Sharp Design')
axes[0].set_ylabel('Coefficient')
axes[0].set_xlabel('Method')
axes[0].axhline(true_tau, linestyle="--", color="r")
axes[0].tick_params(axis='x', rotation=30)
axes[1].errorbar(
df_fuzzy['method'],
df_fuzzy['coef'],
yerr=(df_fuzzy['coef'] - df_fuzzy['CI lower'], df_fuzzy['CI upper'] - df_fuzzy['coef']),
fmt='o',
capsize=5,
capthick=2
)
axes[1].set_title('Fuzzy Design')
axes[1].set_ylabel('Coefficient')
axes[1].set_xlabel('Method')
axes[1].axhline(true_tau, linestyle="--", color="r")
axes[1].tick_params(axis='x', rotation=30)
plt.tight_layout()