Note

Download Jupyter notebook: https://docs.doubleml.org/stable/examples/py_double_ml_basic_iv.ipynb.

Python: Basic Instrumental Variables calculation

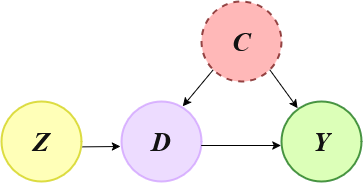
In this example we show how to use the DoubleML functionality of Instrumental Variables (IVs) in the basic setting shown in the graph below, where:

• Z is the instrument

• C is a vector of unobserved confounders

• D is the decision or treatment variable

• Y is the outcome

So, we will first generate synthetic data using linear models compatible with the diagram, and then use the DoubleML package to estimate the causal effect from D to Y.

We assume that you have basic knowledge of instrumental variables and linear regression.

from numpy.random import seed, normal, binomial, uniform
from pandas import DataFrame
from sklearn.linear_model import LinearRegression, LogisticRegression
import doubleml as dml

seed(1234)

Instrumental Variables Directed Acyclic Graph (IV - DAG)

Data Simulation

This code generates n samples in which there is a unique binary confounder. The treatment is also a binary variable, while the outcome is a continuous linear model.

The quantity we want to recover using IVs is the decision_impact, which is the impact of the decision variable into the outcome.

n = 1000
instrument_impact = 0.7
decision_impact = - 2

confounder = binomial(1, 0.3, n)
instrument = binomial(1, 0.5, n)
decision = (uniform(0, 1, n) <= instrument_impact*instrument + 0.4*confounder).astype(int)
outcome = 30 + decision_impact*decision + 10 * confounder + normal(0, 2, n)

df = DataFrame({
    'instrument': instrument,
    'decision': decision,
    'outcome': outcome
})

Naive estimation

We can see that if we make a direct estimation of the impact of the decision into the outcome, though the difference of the averages of outcomes between the two decision groups, we obtain a biased estimate.

outcome_1 = df[df.decision==1].outcome.mean()
outcome_0 = df[df.decision==0].outcome.mean()
print(outcome_1 - outcome_0)

1.1099472942084532

Using DoubleML

DoubleML assumes that there is at least one observed confounder. For this reason, we create a fake variable that doesn’t bring any kind of information to the model, called obs_confounder.

To use the DoubleML we need to specify the Machine Learning methods we want to use to estimate the different relationships between variables:

• ml_g models the functional relationship betwen the outcome and the pair instrument and observed confounders obs_confounders. In this case we choose a LinearRegression because the outcome is continuous.

• ml_m models the functional relationship betwen the obs_confounders and the instrument. In this case we choose a LogisticRegression because the outcome is dichotomic.

• ml_r models the functional relationship betwen the decision and the pair instrument and observed confounders obs_confounders. In this case we choose a LogisticRegression because the outcome is dichotomic.

Notice that instead of using linear and logistic regression, we could use more flexible models capable of dealing with non-linearities such as random forests, boosting, …

df['obs_confounders'] = 1

ml_g = LinearRegression()
ml_m = LogisticRegression(penalty=None)
ml_r = LogisticRegression(penalty=None)

obj_dml_data = dml.DoubleMLData(
    df, y_col='outcome', d_cols='decision',
    z_cols='instrument', x_cols='obs_confounders'
)
dml_iivm_obj = dml.DoubleMLIIVM(obj_dml_data, ml_g, ml_m, ml_r)
print(dml_iivm_obj.fit().summary)

              coef   std err         t     P>|t|    2.5 %    97.5 %
decision -1.917092  0.487533 -3.932227  0.000084 -2.87264 -0.961544

We can see that the causal effect is estimated without bias.

References

Ruiz de Villa, A. Causal Inference for Data Science, Manning Publications, 2024.