Note
-
Download Jupyter notebook:
https://docs.doubleml.org/stable/examples/py_double_ml_pension_qte.ipynb.
Python: Impact of 401(k) on Financial Wealth (Quantile Effects)#
In this real-data example, we illustrate how the DoubleML package can be used to estimate the effect of 401(k) eligibility and participation on accumulated assets. The 401(k) data set has been analyzed in several studies, among others Chernozhukov et al. (2018), see Kallus et al. (2019) for quantile effects.
Remark: This notebook focuses on the evaluation of the treatment effect at different quantiles. For a basic introduction to the DoubleML package and a detailed example of the average treatment effect estimation for the 401(k) data set, we refer to the notebook Python: Impact of 401(k) on Financial Wealth. The Data sections of both notebooks coincide.
401(k) plans are pension accounts sponsored by employers. The key problem in determining the effect of participation in 401(k) plans on accumulated assets is saver heterogeneity coupled with the fact that the decision to enroll in a 401(k) is non-random. It is generally recognized that some people have a higher preference for saving than others. It also seems likely that those individuals with high unobserved preference for saving would be most likely to choose to participate in tax-advantaged retirement savings plans and would tend to have otherwise high amounts of accumulated assets. The presence of unobserved savings preferences with these properties then implies that conventional estimates that do not account for saver heterogeneity and endogeneity of participation will be biased upward, tending to overstate the savings effects of 401(k) participation.
One can argue that eligibility for enrolling in a 401(k) plan in this data can be taken as exogenous after conditioning on a few observables of which the most important for their argument is income. The basic idea is that, at least around the time 401(k)’s initially became available, people were unlikely to be basing their employment decisions on whether an employer offered a 401(k) but would instead focus on income and other aspects of the job.
Data#
The preprocessed data can be fetched by calling fetch_401K(). Note that an internet connection is required for loading the data.
[1]:
import numpy as np
import pandas as pd
import doubleml as dml
import multiprocessing
from doubleml.datasets import fetch_401K
from sklearn.base import clone
from lightgbm import LGBMClassifier, LGBMRegressor
import matplotlib.pyplot as plt
import seaborn as sns
[2]:
sns.set()
colors = sns.color_palette()
[3]:
plt.rcParams['figure.figsize'] = 10., 7.5
sns.set(font_scale=1.5)
sns.set_style('whitegrid', {'axes.spines.top': False,
'axes.spines.bottom': False,
'axes.spines.left': False,
'axes.spines.right': False})
[4]:
data = fetch_401K(return_type='DataFrame')
[5]:
print(data.describe())
nifa net_tfa tw age inc \
count 9.915000e+03 9.915000e+03 9.915000e+03 9915.000000 9915.000000
mean 1.392864e+04 1.805153e+04 6.381685e+04 41.060212 37200.621094
std 5.490488e+04 6.352250e+04 1.115297e+05 10.344505 24774.289062
min 0.000000e+00 -5.023020e+05 -5.023020e+05 25.000000 -2652.000000
25% 2.000000e+02 -5.000000e+02 3.291500e+03 32.000000 19413.000000
50% 1.635000e+03 1.499000e+03 2.510000e+04 40.000000 31476.000000
75% 8.765500e+03 1.652450e+04 8.148750e+04 48.000000 48583.500000
max 1.430298e+06 1.536798e+06 2.029910e+06 64.000000 242124.000000
fsize educ db marr twoearn \
count 9915.000000 9915.000000 9915.000000 9915.000000 9915.000000
mean 2.865860 13.206253 0.271004 0.604841 0.380837
std 1.538937 2.810382 0.444500 0.488909 0.485617
min 1.000000 1.000000 0.000000 0.000000 0.000000
25% 2.000000 12.000000 0.000000 0.000000 0.000000
50% 3.000000 12.000000 0.000000 1.000000 0.000000
75% 4.000000 16.000000 1.000000 1.000000 1.000000
max 13.000000 18.000000 1.000000 1.000000 1.000000
e401 p401 pira hown
count 9915.000000 9915.000000 9915.000000 9915.000000
mean 0.371357 0.261624 0.242158 0.635199
std 0.483192 0.439541 0.428411 0.481399
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 0.000000
50% 0.000000 0.000000 0.000000 1.000000
75% 1.000000 1.000000 0.000000 1.000000
max 1.000000 1.000000 1.000000 1.000000
The data consist of 9,915 observations at the household level drawn from the 1991 Survey of Income and Program Participation (SIPP). All the variables are referred to 1990. We use net financial assets (net_tfa) as the outcome variable, \(Y\), in our analysis. The net financial assets are computed as the sum of IRA balances, 401(k) balances, checking accounts, saving bonds, other interest-earning accounts, other interest-earning assets, stocks, and mutual funds less non mortgage debts.
Among the \(9915\) individuals, \(3682\) are eligible to participate in the program. The variable e401 indicates eligibility and p401 indicates participation, respectively.
At first consider eligibility as the treatment and define the following data.
[6]:
# Set up basic model: Specify variables for data-backend
features_base = ['age', 'inc', 'educ', 'fsize', 'marr',
'twoearn', 'db', 'pira', 'hown']
# Initialize DoubleMLData (data-backend of DoubleML)
data_dml_base = dml.DoubleMLData(data,
y_col='net_tfa',
d_cols='e401',
x_cols=features_base)
Estimating Potential Quantiles and Quantile Treatment Effects#
We will use the DoubleML package to estimate quantile treatment effects of 401(k) eligibility, i.e. e401. As it is more interesting to take a look at a range of quantiles instead of a single one, we will first define a discretisized grid of quanitles tau_vec, which will range from the 10%-quantile to the 90%-quantile. Further, we need a machine learning algorithm to estimate the nuisance elements of our model. In this example, we will use
a basic LGBMClassifier.
[7]:
tau_vec = np.arange(0.1,0.95,0.05)
n_folds = 5
# Learners
class_learner = LGBMClassifier(n_estimators=300, learning_rate=0.05, num_leaves=10, verbose=-1, n_jobs=1)
reg_learner = LGBMRegressor(n_estimators=300, learning_rate=0.05, num_leaves=10, verbose=-1, n_jobs=1)
Next, we will apply create an DoubleMLPQ object for each quantile to fit a quantile model. Here, we have to specifiy, whether we would like to estimate a potential quantile for the treatment group treatment=1 or control treatment=0. Further basic options are trimming and normalization of the propensity scores (trimming_rule="truncate", trimming_threshold=0.01 and normalize_ipw=True).
[8]:
PQ_0 = np.full((len(tau_vec)), np.nan)
PQ_1 = np.full((len(tau_vec)), np.nan)
ci_PQ_0 = np.full((len(tau_vec),2), np.nan)
ci_PQ_1 = np.full((len(tau_vec),2), np.nan)
for idx_tau, tau in enumerate(tau_vec):
print(f'Quantile: {tau}')
dml_PQ_0 = dml.DoubleMLPQ(data_dml_base,
ml_g=clone(class_learner),
ml_m=clone(class_learner),
score="PQ",
treatment=0,
quantile=tau,
n_folds=n_folds,
normalize_ipw=True,
trimming_rule="truncate",
trimming_threshold=1e-2)
dml_PQ_1 = dml.DoubleMLPQ(data_dml_base,
ml_g=clone(class_learner),
ml_m=clone(class_learner),
score="PQ",
treatment=1,
quantile=tau,
n_folds=n_folds,
normalize_ipw=True,
trimming_rule="truncate",
trimming_threshold=1e-2)
dml_PQ_0.fit()
dml_PQ_1.fit()
PQ_0[idx_tau] = dml_PQ_0.coef[0]
PQ_1[idx_tau] = dml_PQ_1.coef[0]
ci_PQ_0[idx_tau, :] = dml_PQ_0.confint(level=0.95).to_numpy()
ci_PQ_1[idx_tau, :] = dml_PQ_1.confint(level=0.95).to_numpy()
Quantile: 0.1
Quantile: 0.15000000000000002
Quantile: 0.20000000000000004
Quantile: 0.25000000000000006
Quantile: 0.30000000000000004
Quantile: 0.3500000000000001
Quantile: 0.40000000000000013
Quantile: 0.45000000000000007
Quantile: 0.5000000000000001
Quantile: 0.5500000000000002
Quantile: 0.6000000000000002
Quantile: 0.6500000000000001
Quantile: 0.7000000000000002
Quantile: 0.7500000000000002
Quantile: 0.8000000000000002
Quantile: 0.8500000000000002
Quantile: 0.9000000000000002
Additionally, each DoubleMLPQ object has a (hopefully) helpful summary, which indicates also the evaluation of the nuisance elements with cross-validated estimation. See e.g. `dml_PQ_1’
[9]:
print(dml_PQ_1)
================== DoubleMLPQ Object ==================
------------------ Data Summary ------------------
Outcome variable: net_tfa
Treatment variable(s): ['e401']
Covariates: ['age', 'inc', 'educ', 'fsize', 'marr', 'twoearn', 'db', 'pira', 'hown']
Instrument variable(s): None
No. Observations: 9915
------------------ Score & Algorithm ------------------
Score function: PQ
------------------ Machine Learner ------------------
Learner ml_g: LGBMClassifier(learning_rate=0.05, n_estimators=300, n_jobs=1, num_leaves=10,
verbose=-1)
Learner ml_m: LGBMClassifier(learning_rate=0.05, n_estimators=300, n_jobs=1, num_leaves=10,
verbose=-1)
Out-of-sample Performance:
Classification:
Learner ml_g Log Loss: [[0.33168943]]
Learner ml_m Log Loss: [[0.57751232]]
------------------ Resampling ------------------
No. folds: 5
No. repeated sample splits: 1
------------------ Fit Summary ------------------
coef std err t P>|t| 2.5 % \
e401 63499.0 1888.230821 33.628834 6.358690e-248 59798.135596
97.5 %
e401 67199.864404
Finally, let us take a look at the estimated potential quantiles
[10]:
data_pq = {"Quantile": tau_vec,
"DML Y(0)": PQ_0, "DML Y(1)": PQ_1,
"DML Y(0) lower": ci_PQ_0[:, 0], "DML Y(0) upper": ci_PQ_0[:, 1],
"DML Y(1) lower": ci_PQ_1[:, 0], "DML Y(1) upper": ci_PQ_1[:, 1]}
df_pq = pd.DataFrame(data_pq)
print(df_pq)
Quantile DML Y(0) DML Y(1) DML Y(0) lower DML Y(0) upper \
0 0.10 -5.320000e+03 -3.978000e+03 -5708.039154 -4931.960846
1 0.15 -3.200000e+03 -2.000000e+03 -3422.338855 -2977.661145
2 0.20 -2.000000e+03 -7.270000e+02 -2167.843296 -1832.156704
3 0.25 -1.000000e+03 -1.077527e-12 -1144.513658 -855.486342
4 0.30 -3.480000e+02 2.800000e+02 -485.671633 -210.328367
5 0.35 -1.063428e-12 1.000000e+03 -140.524215 140.524215
6 0.40 1.512657e-12 1.425000e+03 -141.848578 141.848578
7 0.45 1.000000e+02 3.648000e+03 -43.070797 243.070797
8 0.50 5.000000e+02 4.450000e+03 354.370165 645.629835
9 0.55 1.200000e+03 6.450000e+03 1040.412406 1359.587594
10 0.60 2.398000e+03 9.500000e+03 2175.942629 2620.057371
11 0.65 4.100000e+03 1.370000e+04 3712.348338 4487.651662
12 0.70 6.499000e+03 1.790000e+04 5804.239845 7193.760155
13 0.75 1.074700e+04 2.330000e+04 9773.014721 11720.985279
14 0.80 1.600000e+04 3.320000e+04 14530.490898 17469.509102
15 0.85 2.564800e+04 4.496300e+04 23368.042583 27927.957417
16 0.90 4.190000e+04 6.349900e+04 38348.193833 45451.806167
DML Y(1) lower DML Y(1) upper
0 -4584.205245 -3371.794755
1 -2445.618722 -1554.381278
2 -1275.916921 -178.083079
3 -412.409390 412.409390
4 -179.647750 739.647750
5 413.167035 1586.832965
6 843.522605 2006.477395
7 2760.562866 4535.437134
8 3598.463208 5301.536792
9 5494.106116 7405.893884
10 8208.841712 10791.158288
11 11850.483855 15549.516145
12 16249.111783 19550.888217
13 20956.028868 25643.971132
14 30186.784841 36213.215159
15 42143.373235 47782.626765
16 59798.135596 67199.864404
[11]:
from matplotlib import pyplot as plt
plt.rcParams['figure.figsize'] = 10., 7.5
fig, (ax1, ax2) = plt.subplots(1 ,2)
ax1.grid(visible=True); ax2.grid(visible=True)
ax1.plot(df_pq['Quantile'],df_pq['DML Y(0)'], color='violet', label='Estimated Quantile Y(0)')
ax1.fill_between(df_pq['Quantile'], df_pq['DML Y(0) lower'], df_pq['DML Y(0) upper'], color='violet', alpha=.3, label='Confidence Interval')
ax1.legend()
ax2.plot(df_pq['Quantile'],df_pq['DML Y(1)'], color='violet', label='Estimated Quantile Y(1)')
ax2.fill_between(df_pq['Quantile'], df_pq['DML Y(1) lower'], df_pq['DML Y(1) upper'], color='violet', alpha=.3, label='Confidence Interval')
ax2.legend()
fig.suptitle('Potential Quantiles', fontsize=16)
fig.supxlabel('Quantile')
_ = fig.supylabel('Potential Quantile and 95%-CI')
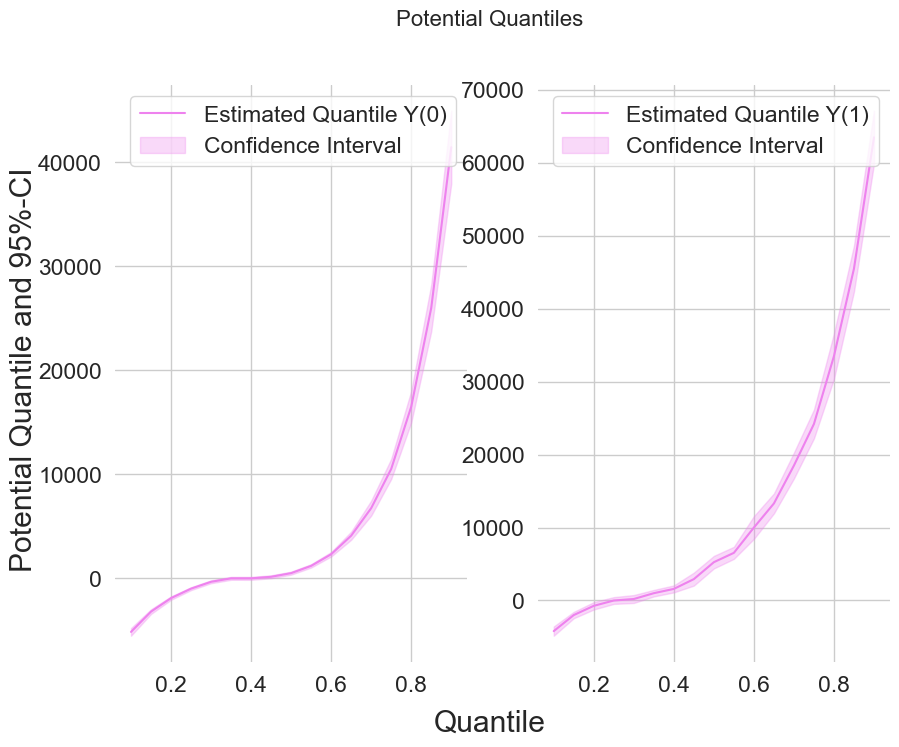
As we are interested in the QTE, we can use the DoubleMLQTE object, which internally fits two DoubleMLPQ objects for the treatment and control group. The main advantage is to apply this to a list of quantiles and construct uniformly valid confidence intervals for the range of treatment effects.
[12]:
n_cores = multiprocessing.cpu_count()
cores_used = np.min([5, n_cores - 1])
print(f"Number of Cores used: {cores_used}")
np.random.seed(42)
dml_QTE = dml.DoubleMLQTE(data_dml_base,
ml_g=clone(class_learner),
ml_m=clone(class_learner),
quantiles=tau_vec,
score='PQ',
n_folds=n_folds,
normalize_ipw=True,
trimming_rule="truncate",
trimming_threshold=1e-2)
dml_QTE.fit(n_jobs_models=cores_used)
print(dml_QTE)
Number of Cores used: 5
================== DoubleMLQTE Object ==================
------------------ Fit summary ------------------
coef std err t P>|t| 2.5 % \
0.10 1210.0 486.438569 2.487467 1.286563e-02 256.597923
0.15 1230.0 263.748513 4.663533 3.108257e-06 713.062414
0.20 1211.0 252.052811 4.804549 1.551010e-06 716.985569
0.25 1000.0 244.841847 4.084269 4.421576e-05 520.118799
0.30 622.0 255.252133 2.436806 1.481761e-02 121.715013
0.35 1031.0 274.813682 3.751633 1.756867e-04 492.375081
0.40 2006.0 320.163566 6.265547 3.715179e-10 1378.490941
0.45 3329.0 427.336461 7.790115 6.661338e-15 2491.435927
0.50 4601.0 448.109454 10.267581 0.000000e+00 3722.721609
0.55 6000.0 590.561309 10.159826 0.000000e+00 4842.521104
0.60 7040.0 605.739720 11.622153 0.000000e+00 5852.771965
0.65 9243.0 809.469379 11.418591 0.000000e+00 7656.469170
0.70 10928.0 859.705581 12.711328 0.000000e+00 9243.008023
0.75 12410.0 1018.114834 12.189195 0.000000e+00 10414.531594
0.80 16590.0 1589.396531 10.437924 0.000000e+00 13474.840041
0.85 19382.0 1622.701413 11.944280 0.000000e+00 16201.563673
0.90 21550.0 2279.055439 9.455672 0.000000e+00 17083.133421
97.5 %
0.10 2163.402077
0.15 1746.937586
0.20 1705.014431
0.25 1479.881201
0.30 1122.284987
0.35 1569.624919
0.40 2633.509059
0.45 4166.564073
0.50 5479.278391
0.55 7157.478896
0.60 8227.228035
0.65 10829.530830
0.70 12612.991977
0.75 14405.468406
0.80 19705.159959
0.85 22562.436327
0.90 26016.866579
For uniformly valid confidence intervals, we still need to apply a bootstrap first. Let’s take a quick look at the QTEs combinded with a confidence interval.
[13]:
dml_QTE.bootstrap(n_rep_boot=2000)
ci_QTE = dml_QTE.confint(level=0.95, joint=True)
data_qte = {"Quantile": tau_vec, "DML QTE": dml_QTE.coef,
"DML QTE lower": ci_QTE["2.5 %"], "DML QTE upper": ci_QTE["97.5 %"]}
df_qte = pd.DataFrame(data_qte)
print(df_qte)
Quantile DML QTE DML QTE lower DML QTE upper
0.10 0.10 1210.0 -164.794119 2584.794119
0.15 0.15 1230.0 484.582331 1975.417669
0.20 0.20 1211.0 498.637240 1923.362760
0.25 0.25 1000.0 308.017185 1691.982815
0.30 0.30 622.0 -99.404824 1343.404824
0.35 0.35 1031.0 254.309464 1807.690536
0.40 0.40 2006.0 1101.139622 2910.860378
0.45 0.45 3329.0 2121.242864 4536.757136
0.50 0.50 4601.0 3334.533316 5867.466684
0.55 0.55 6000.0 4330.929607 7669.070393
0.60 0.60 7040.0 5328.031712 8751.968288
0.65 0.65 9243.0 6955.241973 11530.758027
0.70 0.70 10928.0 8498.262204 13357.737796
0.75 0.75 12410.0 9532.558996 15287.441004
0.80 0.80 16590.0 12097.977489 21082.022511
0.85 0.85 19382.0 14795.849766 23968.150234
0.90 0.90 21550.0 15108.833096 27991.166904
[14]:
plt.rcParams['figure.figsize'] = 10., 7.5
fig, ax = plt.subplots()
ax.grid(visible=True)
ax.plot(df_qte['Quantile'],df_qte['DML QTE'], color='violet', label='Estimated QTE')
ax.fill_between(df_qte['Quantile'], df_qte['DML QTE lower'], df_qte['DML QTE upper'], color='violet', alpha=.3, label='Confidence Interval')
plt.legend()
plt.title('Quantile Treatment Effects', fontsize=16)
plt.xlabel('Quantile')
_ = plt.ylabel('QTE and 95%-CI')
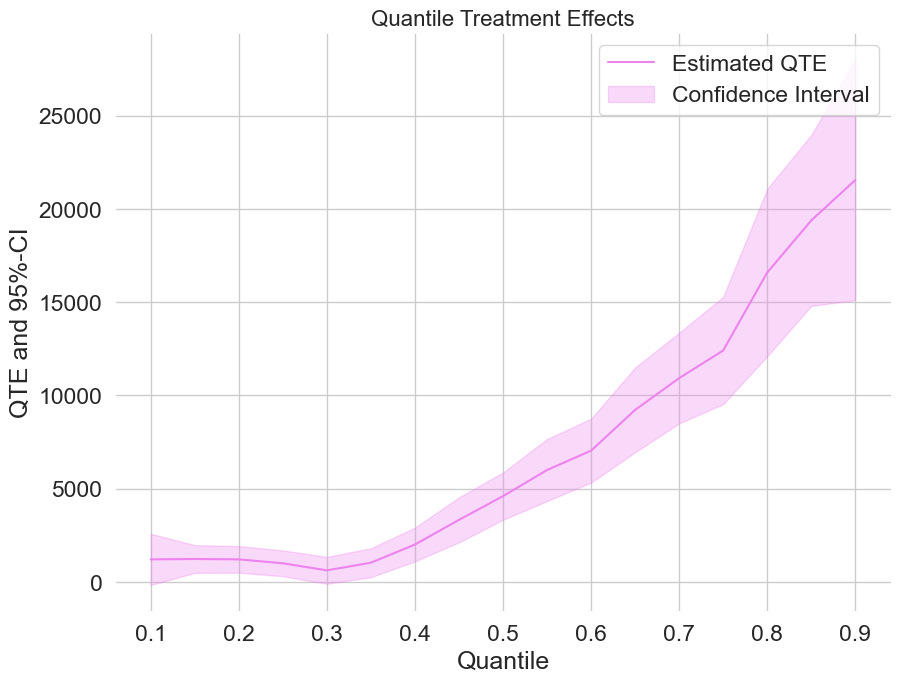
Estimating the treatment effect on the Conditional Value a Risk (CVaR)#
Similar to the evaluation of the estimation of quantile treatment effects (QTEs), we can estimate the conditional value at risk (CVaR) for given quantiles. Here, we will only focus on treatment effect estimation, but the DoubleML package also allows for estimation of potential CVaRs.
The estimation of treatment effects can be easily done by adjusting the score in the DoubleMLQTE object to score="CVaR", as the estimation is based on the same nuisance elements as QTEs.
[15]:
np.random.seed(42)
dml_CVAR = dml.DoubleMLQTE(data_dml_base,
ml_g=clone(reg_learner),
ml_m=clone(class_learner),
quantiles=tau_vec,
score="CVaR",
n_folds=n_folds,
normalize_ipw=True,
trimming_rule="truncate",
trimming_threshold=1e-2)
dml_CVAR.fit(n_jobs_models=cores_used)
print(dml_CVAR)
================== DoubleMLQTE Object ==================
------------------ Fit summary ------------------
coef std err t P>|t| 2.5 % \
0.10 9045.771876 1297.433473 6.972051 3.123501e-12 6502.848997
0.15 10126.150435 1371.682315 7.382285 1.556533e-13 7437.702500
0.20 14588.483642 1485.887212 9.818029 0.000000e+00 11676.198221
0.25 16910.113005 1582.022950 10.688918 0.000000e+00 13809.405000
0.30 14744.693345 1676.606733 8.794366 0.000000e+00 11458.604532
0.35 16241.220211 1812.325046 8.961538 0.000000e+00 12689.128393
0.40 18666.064164 1970.604110 9.472255 0.000000e+00 14803.751081
0.45 12861.546438 2086.920695 6.162930 7.141101e-10 8771.257037
0.50 13642.272643 2295.693359 5.942550 2.806220e-09 9142.796340
0.55 14772.076119 2543.121297 5.808640 6.298235e-09 9787.649969
0.60 15556.470365 2849.994864 5.458420 4.803889e-08 9970.583076
0.65 16618.635757 3235.158198 5.136885 2.793297e-07 10277.842205
0.70 17576.744211 3745.384883 4.692907 2.693495e-06 10235.924732
0.75 18773.183814 4438.392472 4.229726 2.339762e-05 10074.094420
0.80 19798.478399 5475.067639 3.616116 2.990567e-04 9067.543014
0.85 19824.886611 7155.563760 2.770556 5.596076e-03 5800.239352
0.90 20055.810916 10406.538282 1.927232 5.395076e-02 -340.629319
97.5 %
0.10 11588.694755
0.15 12814.598371
0.20 17500.769063
0.25 20010.821009
0.30 18030.782159
0.35 19793.312030
0.40 22528.377246
0.45 16951.835839
0.50 18141.748945
0.55 19756.502268
0.60 21142.357654
0.65 22959.429309
0.70 24917.563690
0.75 27472.273208
0.80 30529.413784
0.85 33849.533871
0.90 40452.251152
Estimation of the corresponding (uniformly) valid confidence intervals can be done analogously to the quantile treatment effects.
[16]:
dml_CVAR.bootstrap(n_rep_boot=2000)
ci_CVAR = dml_CVAR.confint(level=0.95, joint=True)
data_cvar = {"Quantile": tau_vec, "DML CVAR": dml_CVAR.coef,
"DML CVAR lower": ci_CVAR["2.5 %"], "DML CVAR upper": ci_CVAR["97.5 %"]}
df_cvar = pd.DataFrame(data_cvar)
print(df_cvar)
Quantile DML CVAR DML CVAR lower DML CVAR upper
0.10 0.10 9045.771876 6241.250083 11850.293669
0.15 0.15 10126.150435 7161.132941 13091.167930
0.20 0.20 14588.483642 11376.601757 17800.365527
0.25 0.25 16910.113005 13490.424879 20329.801130
0.30 0.30 14744.693345 11120.553672 18368.833018
0.35 0.35 16241.220211 12323.712921 20158.727501
0.40 0.40 18666.064164 14406.422119 22925.706208
0.45 0.45 12861.546438 8350.475395 17372.617481
0.50 0.50 13642.272643 8679.920283 18604.625002
0.55 0.55 14772.076119 9274.885513 20269.266724
0.60 0.60 15556.470365 9395.944317 21716.996413
0.65 0.65 16618.635757 9625.543734 23611.727780
0.70 0.70 17576.744211 9480.750275 25672.738147
0.75 0.75 18773.183814 9179.190231 28367.177397
0.80 0.80 19798.478399 7963.616086 31633.340712
0.85 0.85 19824.886611 4357.477354 35292.295868
0.90 0.90 20055.810916 -2438.878802 42550.500635
Finally, let us take a look at the estimated treatment effects on the CVaR.
[17]:
plt.rcParams['figure.figsize'] = 10., 7.5
fig, ax = plt.subplots()
ax.grid(visible=True)
ax.plot(df_cvar['Quantile'],df_cvar['DML CVAR'], color='violet', label='Estimated CVaR Effect')
ax.fill_between(df_cvar['Quantile'], df_cvar['DML CVAR lower'], df_cvar['DML CVAR upper'], color='violet', alpha=.3, label='Confidence Interval')
plt.legend()
plt.title('Conditional Value at Risk', fontsize=16)
plt.xlabel('Quantile')
_ = plt.ylabel('CVaR Effect and 95%-CI')
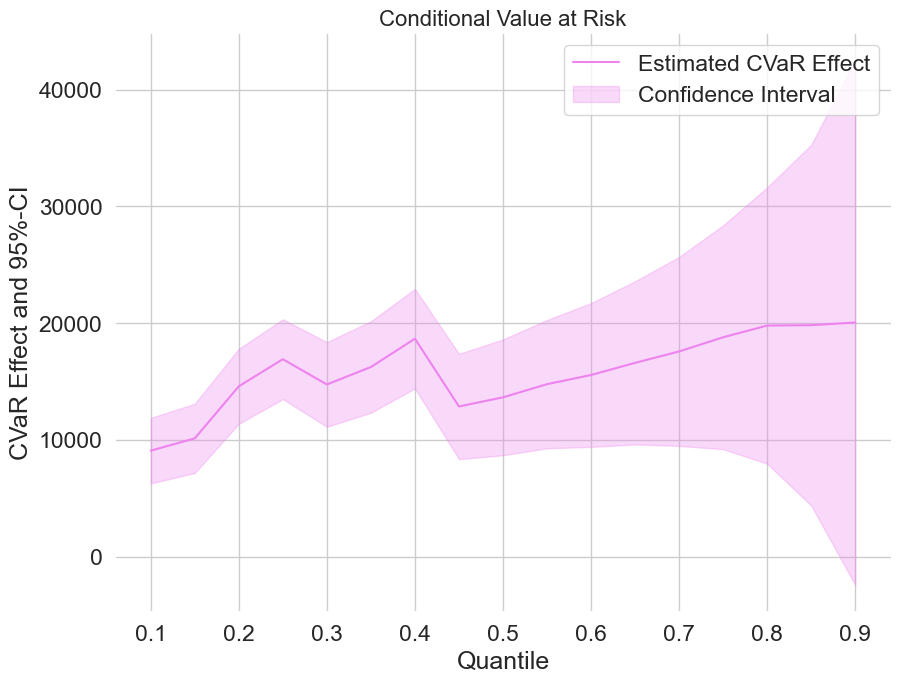
Estimating local quantile treatment effects (LQTEs)#
If we have an IIVM model with a given instrumental variable, we are still able to identify the local quantile treatment effect (LQTE), the quantile treatment effect on compliers. For the 401(k) pension data we can use e401 as an instrument for participation p401. To fit an DoubleML model with an instrument, we have to change the data backend and specify the instrument.
[18]:
# Initialize DoubleMLData with an instrument
# Basic model
data_dml_base_iv = dml.DoubleMLData(data,
y_col='net_tfa',
d_cols='p401',
z_cols='e401',
x_cols=features_base)
print(data_dml_base_iv)
================== DoubleMLData Object ==================
------------------ Data summary ------------------
Outcome variable: net_tfa
Treatment variable(s): ['p401']
Covariates: ['age', 'inc', 'educ', 'fsize', 'marr', 'twoearn', 'db', 'pira', 'hown']
Instrument variable(s): ['e401']
No. Observations: 9915
------------------ DataFrame info ------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 9915 entries, 0 to 9914
Columns: 14 entries, nifa to hown
dtypes: float32(4), int8(10)
memory usage: 251.9 KB
The estimation of local treatment effects can be easily done by adjusting the score in the DoubleMLQTE object to score="LPQ".
[19]:
np.random.seed(42)
dml_LQTE = dml.DoubleMLQTE(data_dml_base_iv,
ml_g=clone(class_learner),
ml_m=clone(class_learner),
quantiles=tau_vec,
score="LPQ",
n_folds=n_folds,
normalize_ipw=True,
trimming_rule="truncate",
trimming_threshold=1e-2)
dml_LQTE.fit(n_jobs_models=cores_used)
print(dml_LQTE)
================== DoubleMLQTE Object ==================
------------------ Fit summary ------------------
coef std err t P>|t| 2.5 % \
0.10 2610.0 487.820993 5.350323 8.779727e-08 1653.888423
0.15 1773.0 357.148835 4.964317 6.894329e-07 1073.001145
0.20 1398.0 386.526532 3.616828 2.982353e-04 640.421919
0.25 1435.0 384.956574 3.727693 1.932404e-04 680.498979
0.30 1400.0 436.977295 3.203828 1.356136e-03 543.540240
0.35 2500.0 486.877153 5.134765 2.824961e-07 1545.738315
0.40 3985.0 596.725087 6.678117 2.420308e-11 2815.440320
0.45 5175.0 739.887778 6.994304 2.665868e-12 3724.846602
0.50 7239.0 775.751013 9.331602 0.000000e+00 5718.555954
0.55 9500.0 1109.046788 8.565915 0.000000e+00 7326.308239
0.60 11750.0 1295.711518 9.068377 0.000000e+00 9210.452091
0.65 14625.0 1443.080854 10.134567 0.000000e+00 11796.613498
0.70 16984.0 1576.564577 10.772791 0.000000e+00 13893.990210
0.75 19758.0 2865.426736 6.895308 5.374812e-12 14141.866798
0.80 23856.0 2281.099670 10.458114 0.000000e+00 19385.126802
0.85 27066.0 2920.063312 9.268977 0.000000e+00 21342.781076
0.90 30645.0 4634.200110 6.612792 3.771383e-11 21562.134687
97.5 %
0.10 3566.111577
0.15 2472.998855
0.20 2155.578081
0.25 2189.501021
0.30 2256.459760
0.35 3454.261685
0.40 5154.559680
0.45 6625.153398
0.50 8759.444046
0.55 11673.691761
0.60 14289.547909
0.65 17453.386502
0.70 20074.009790
0.75 25374.133202
0.80 28326.873198
0.85 32789.218924
0.90 39727.865313
Estimation of the corresponding (uniformly) valid confidence intervals can be done analogously to the quantile treatment effects.
[20]:
dml_LQTE.bootstrap(n_rep_boot=2000)
ci_LQTE = dml_LQTE.confint(level=0.95, joint=True)
data_lqte = {"Quantile": tau_vec, "DML LQTE": dml_LQTE.coef,
"DML LQTE lower": ci_LQTE["2.5 %"], "DML LQTE upper": ci_LQTE["97.5 %"]}
df_lqte = pd.DataFrame(data_lqte)
print(df_lqte)
Quantile DML LQTE DML LQTE lower DML LQTE upper
0.10 0.10 2610.0 1258.618753 3961.381247
0.15 0.15 1773.0 783.611995 2762.388005
0.20 0.20 1398.0 327.228725 2468.771275
0.25 0.25 1435.0 368.577884 2501.422116
0.30 0.30 1400.0 189.468001 2610.531999
0.35 0.35 2500.0 1151.233415 3848.766585
0.40 0.40 3985.0 2331.928269 5638.071731
0.45 0.45 5175.0 3125.333250 7224.666750
0.50 0.50 7239.0 5089.983482 9388.016518
0.55 0.55 9500.0 6427.674181 12572.325819
0.60 0.60 11750.0 8160.568071 15339.431929
0.65 0.65 14625.0 10627.319634 18622.680366
0.70 0.70 16984.0 12616.537681 21351.462319
0.75 0.75 19758.0 11820.080121 27695.919879
0.80 0.80 23856.0 17536.806356 30175.193644
0.85 0.85 27066.0 18976.723689 35155.276311
0.90 0.90 30645.0 17807.153293 43482.846707
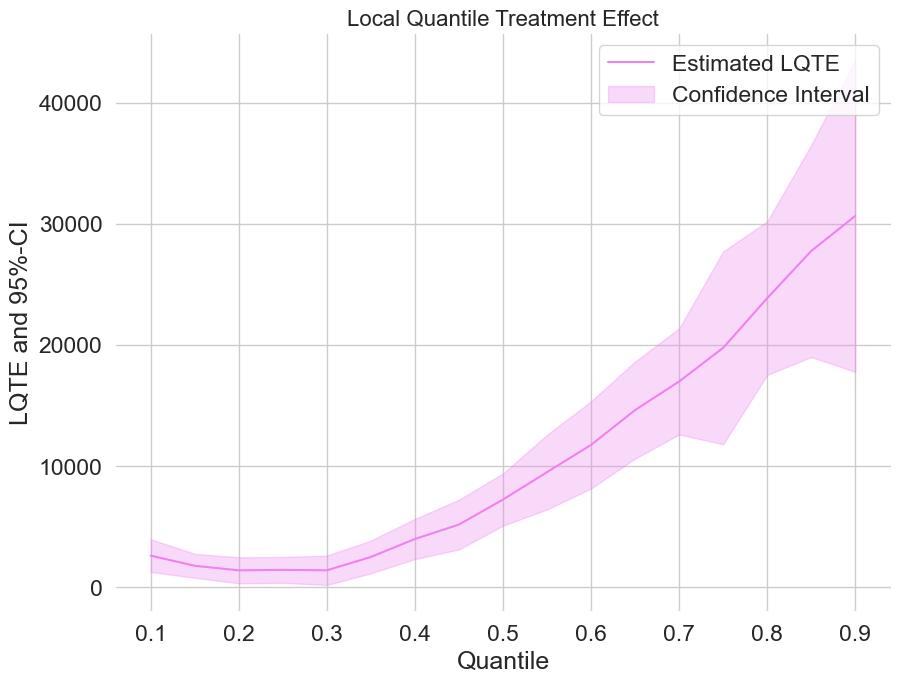
Finally, let us take a look at the estimated local quantile treatment effects.
[21]:
plt.rcParams['figure.figsize'] = 10., 7.5
fig, ax = plt.subplots()
ax.grid(visible=True)
ax.plot(df_lqte['Quantile'],df_lqte['DML LQTE'], color='violet', label='Estimated LQTE')
ax.fill_between(df_lqte['Quantile'], df_lqte['DML LQTE lower'], df_lqte['DML LQTE upper'], color='violet', alpha=.3, label='Confidence Interval')
plt.legend()
plt.title('Local Quantile Treatment Effect', fontsize=16)
plt.xlabel('Quantile')
_ = plt.ylabel('LQTE and 95%-CI')