Note
-
Download Jupyter notebook:
https://docs.doubleml.org/stable/examples/py_double_ml_cate_plr.ipynb.
Python: Conditional Average Treatment Effects (CATEs) for PLR models#
In this simple example, we illustrate how the DoubleML package can be used to estimate conditional average treatment effects with B-splines for one or two-dimensional effects in the DoubleMLPLR model.
[1]:
import numpy as np
import pandas as pd
import doubleml as dml
from doubleml.datasets import make_heterogeneous_data
Data#
We define a data generating process to create synthetic data to compare the estimates to the true effect. The data generating process is based on the Monte Carlo simulation from Oprescu et al. (2019).
The documentation of the data generating process can be found here.
One-dimensional Example#
We start with an one-dimensional effect and create our training data. In this example the true effect depends only the first covariate \(X_0\) and takes the following form
The generated dictionary also contains a callable with key treatment_effect to calculate the true treatment effect for new observations.
[2]:
np.random.seed(42)
data_dict = make_heterogeneous_data(
n_obs=2000,
p=10,
support_size=5,
n_x=1,
)
treatment_effect = data_dict['treatment_effect']
data = data_dict['data']
print(data.head())
y d X_0 X_1 X_2 X_3 X_4 \
0 1.564451 0.241064 0.259828 0.886086 0.895690 0.297287 0.229994
1 1.114570 0.040912 0.824350 0.396992 0.156317 0.737951 0.360475
2 8.901013 1.392623 0.988421 0.977280 0.793818 0.659423 0.577807
3 -1.315155 -0.551317 0.427486 0.330285 0.564232 0.850575 0.201528
4 1.314625 0.683487 0.016200 0.818380 0.040139 0.889913 0.991963
X_5 X_6 X_7 X_8 X_9
0 0.411304 0.240532 0.672384 0.826065 0.673092
1 0.671271 0.270644 0.081230 0.992582 0.156202
2 0.866102 0.289440 0.467681 0.619390 0.411190
3 0.934433 0.689088 0.823273 0.556191 0.779517
4 0.294067 0.210319 0.765363 0.253026 0.865562
First, define the DoubleMLData object.
[3]:
data_dml_base = dml.DoubleMLData(
data,
y_col='y',
d_cols='d'
)
Next, define the learners for the nuisance functions and fit the PLR Model. Remark that linear learners would usually be optimal due to the data generating process.
[4]:
# First stage estimation
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
ml_l = RandomForestRegressor(n_estimators=500)
ml_m = RandomForestRegressor(n_estimators=500)
np.random.seed(42)
dml_plr = dml.DoubleMLPLR(data_dml_base,
ml_l=ml_l,
ml_m=ml_m,
n_folds=5)
print("Training PLR Model")
dml_plr.fit()
print(dml_plr.summary)
Training PLR Model
coef std err t P>|t| 2.5 % 97.5 %
d 4.377669 0.043998 99.497422 0.0 4.291434 4.463903
To estimate the CATE, we rely on the best-linear-predictor of the linear score as in Semenova et al. (2021) To approximate the target function \(\theta_0(x)\) with a linear form, we have to define a data frame of basis functions. Here, we rely on patsy to construct a suitable basis of B-splines.
[5]:
import patsy
design_matrix = patsy.dmatrix("bs(x, df=5, degree=2)", {"x": data["X_0"]})
spline_basis = pd.DataFrame(design_matrix)
To estimate the parameters to calculate the CATE estimate call the cate() method and supply the dataframe of basis elements.
[6]:
cate = dml_plr.cate(spline_basis)
print(cate)
================== DoubleMLBLP Object ==================
------------------ Fit summary ------------------
coef std err t P>|t| [0.025 0.975]
0 1.239313 0.141002 8.789330 1.504548e-18 0.962954 1.515672
1 1.581849 0.237115 6.671224 2.536778e-11 1.117112 2.046587
2 4.178218 0.156169 26.754499 1.094581e-157 3.872132 4.484303
3 4.040919 0.180262 22.416919 2.691848e-111 3.687612 4.394226
4 3.272408 0.179777 18.202603 4.921256e-74 2.920052 3.624764
5 3.796384 0.182427 20.810419 3.482898e-96 3.438834 4.153935
To obtain the confidence intervals for the CATE, we have to call the confint() method and a supply a dataframe of basis elements. This could be the same basis as for fitting the CATE model or a new basis to e.g. evaluate the CATE model on a grid. Here, we will evaluate the CATE on a grid from 0.1 to 0.9 to plot the final results. Further, we construct uniform confidence intervals by setting the option joint and providing a number of bootstrap repetitions n_rep_boot.
[7]:
new_data = {"x": np.linspace(0.1, 0.9, 100)}
spline_grid = pd.DataFrame(patsy.build_design_matrices([design_matrix.design_info], new_data)[0])
df_cate = cate.confint(spline_grid, level=0.95, joint=True, n_rep_boot=2000)
print(df_cate)
2.5 % effect 97.5 %
0 2.199412 2.429057 2.658702
1 2.289357 2.521611 2.753866
2 2.376806 2.613622 2.850439
3 2.462567 2.705090 2.947613
4 2.547324 2.796014 3.044704
.. ... ... ...
95 4.494089 4.734770 4.975450
96 4.502901 4.738065 4.973229
97 4.514173 4.743341 4.972509
98 4.527452 4.750597 4.973741
99 4.542159 4.759833 4.977507
[100 rows x 3 columns]
Finally, we can plot our results and compare them with the true effect.
[8]:
from matplotlib import pyplot as plt
plt.rcParams['figure.figsize'] = 10., 7.5
df_cate['x'] = new_data['x']
df_cate['true_effect'] = treatment_effect(new_data["x"].reshape(-1, 1))
fig, ax = plt.subplots()
ax.plot(df_cate['x'],df_cate['effect'], label='Estimated Effect')
ax.plot(df_cate['x'],df_cate['true_effect'], color="green", label='True Effect')
ax.fill_between(df_cate['x'], df_cate['2.5 %'], df_cate['97.5 %'], color='b', alpha=.3, label='Confidence Interval')
plt.legend()
plt.title('CATE')
plt.xlabel('x')
_ = plt.ylabel('Effect and 95%-CI')
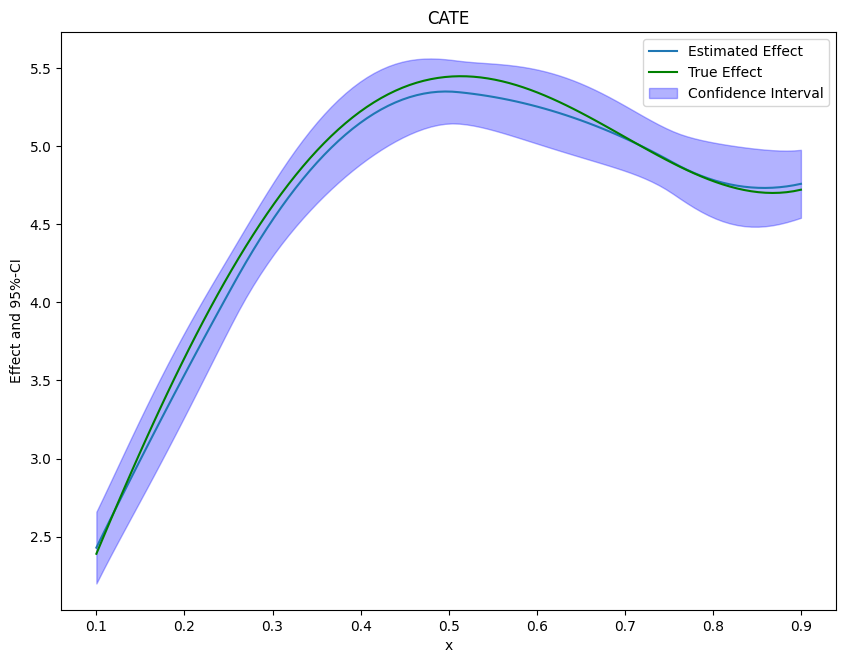
If the effect is not one-dimensional, the estimate still corresponds to the projection of the true effect on the basis functions.
Two-Dimensional Example#
It is also possible to estimate multi-dimensional conditional effects. We will use a similar data generating process but now the effect depends on the first two covariates \(X_0\) and \(X_1\) and takes the following form
With the argument n_x=2 we can specify set the effect to be two-dimensional.
[9]:
np.random.seed(42)
data_dict = make_heterogeneous_data(
n_obs=5000,
p=10,
support_size=5,
n_x=2,
)
treatment_effect = data_dict['treatment_effect']
data = data_dict['data']
print(data.head())
y d X_0 X_1 X_2 X_3 X_4 \
0 -0.359307 -0.479722 0.014080 0.006958 0.240127 0.100807 0.260211
1 0.578557 -0.587135 0.152148 0.912230 0.892796 0.653901 0.672234
2 1.479882 0.172083 0.344787 0.893649 0.291517 0.562712 0.099731
3 4.468072 0.480579 0.619351 0.232134 0.000943 0.757151 0.985207
4 5.949866 0.974213 0.477130 0.447624 0.775191 0.526769 0.316717
X_5 X_6 X_7 X_8 X_9
0 0.177043 0.028520 0.909304 0.008223 0.736082
1 0.005339 0.984872 0.877833 0.895106 0.659245
2 0.921956 0.140770 0.224897 0.558134 0.764093
3 0.809913 0.460207 0.903767 0.409848 0.524934
4 0.258158 0.037747 0.583195 0.229961 0.148134
As univariate example estimate the PLR Model.
[10]:
data_dml_base = dml.DoubleMLData(
data,
y_col='y',
d_cols='d'
)
[11]:
# First stage estimation
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
ml_l = RandomForestRegressor(n_estimators=500)
ml_m = RandomForestRegressor(n_estimators=500)
np.random.seed(42)
dml_plr = dml.DoubleMLPLR(data_dml_base,
ml_l=ml_l,
ml_m=ml_m,
n_folds=5)
print("Training PLR Model")
dml_plr.fit()
print(dml_plr.summary)
Training PLR Model
coef std err t P>|t| 2.5 % 97.5 %
d 4.469895 0.04973 89.883485 0.0 4.372427 4.567364
As above, we will rely on the patsy package to construct the basis elements. In the two-dimensional case, we will construct a tensor product of B-splines (for more information see here).
[12]:
design_matrix = patsy.dmatrix("te(bs(x_0, df=7, degree=3), bs(x_1, df=7, degree=3))", {"x_0": data["X_0"], "x_1": data["X_1"]})
spline_basis = pd.DataFrame(design_matrix)
cate = dml_plr.cate(spline_basis)
print(cate)
================== DoubleMLBLP Object ==================
------------------ Fit summary ------------------
coef std err t P>|t| [0.025 0.975]
0 2.785038 0.171833 16.207834 4.439401e-59 2.448252 3.121824
1 -3.326148 0.855862 -3.886314 1.017777e-04 -5.003607 -1.648690
2 3.068073 0.738876 4.152353 3.290736e-05 1.619903 4.516242
3 1.733047 0.719552 2.408509 1.601783e-02 0.322751 3.143342
4 2.016011 0.675233 2.985654 2.829730e-03 0.692579 3.339443
5 -3.886041 0.865914 -4.487793 7.196478e-06 -5.583201 -2.188882
6 -5.448842 0.933671 -5.835935 5.348980e-09 -7.278804 -3.618881
7 -7.348700 0.933857 -7.869195 3.569315e-15 -9.179026 -5.518375
8 -0.629549 0.797868 -0.789039 4.300892e-01 -2.193341 0.934243
9 -0.213070 0.825587 -0.258083 7.963427e-01 -1.831190 1.405050
10 1.905042 0.732150 2.601984 9.268628e-03 0.470055 3.340029
11 0.572991 0.706077 0.811513 4.170709e-01 -0.810895 1.956877
12 -0.871923 0.888445 -0.981403 3.263942e-01 -2.613244 0.869398
13 -1.231153 0.977202 -1.259875 2.077144e-01 -3.146435 0.684128
14 -2.161049 0.759054 -2.847029 4.412941e-03 -3.648769 -0.673330
15 0.084156 0.768763 0.109470 9.128300e-01 -1.422591 1.590904
16 2.889326 0.706122 4.091824 4.279933e-05 1.505353 4.273299
17 1.899716 0.639603 2.970150 2.976548e-03 0.646117 3.153314
18 2.681246 0.616617 4.348319 1.371850e-05 1.472699 3.889792
19 -1.993201 0.748084 -2.664409 7.712372e-03 -3.459418 -0.526984
20 -1.965341 0.758831 -2.589958 9.598761e-03 -3.452623 -0.478059
21 -4.128651 0.631083 -6.542170 6.063234e-11 -5.365551 -2.891752
22 0.161288 0.788868 0.204455 8.379981e-01 -1.384865 1.707441
23 4.430595 0.767549 5.772396 7.815213e-09 2.926227 5.934963
24 2.308568 0.714250 3.232157 1.228597e-03 0.908663 3.708472
25 3.346269 0.683687 4.894448 9.858212e-07 2.006267 4.686270
26 0.029022 0.811011 0.035785 9.714534e-01 -1.560530 1.618574
27 -1.186237 0.887648 -1.336382 1.814246e-01 -2.925995 0.553522
28 -1.137213 0.917000 -1.240146 2.149215e-01 -2.934500 0.660073
29 5.555137 1.259164 4.411768 1.025300e-05 3.087222 8.023052
30 1.414533 1.078709 1.311321 1.897495e-01 -0.699697 3.528763
31 7.397155 0.959384 7.710319 1.255034e-14 5.516797 9.277512
32 2.910895 0.911277 3.194303 1.401690e-03 1.124825 4.696966
33 2.228630 1.087745 2.048853 4.047652e-02 0.096688 4.360572
34 0.202846 1.156684 0.175369 8.607900e-01 -2.064213 2.469905
35 1.050538 1.063593 0.987726 3.232868e-01 -1.034065 3.135142
36 6.569540 1.290565 5.090436 3.572408e-07 4.040079 9.099001
37 5.115636 1.225350 4.174835 2.982019e-05 2.713993 7.517279
38 7.074617 0.962373 7.351220 1.964065e-13 5.188400 8.960834
39 5.933322 1.177830 5.037504 4.716427e-07 3.624818 8.241827
40 4.316863 1.355651 3.184347 1.450812e-03 1.659835 6.973890
41 1.626633 1.330163 1.222882 2.213743e-01 -0.980440 4.233705
42 -0.761429 1.392128 -0.546953 5.844107e-01 -3.489951 1.967092
43 8.384443 1.385160 6.053049 1.421297e-09 5.669579 11.099307
44 7.251480 1.561348 4.644371 3.411146e-06 4.191294 10.311667
45 8.031820 0.913371 8.793598 1.448456e-18 6.241645 9.821995
46 7.031156 1.135665 6.191223 5.969925e-10 4.805293 9.257019
47 4.639580 1.333955 3.478064 5.050494e-04 2.025077 7.254083
48 2.492656 0.935764 2.663765 7.727159e-03 0.658592 4.326721
49 3.651127 0.538105 6.785153 1.159633e-11 2.596460 4.705794
Finally, we create a new grid to evaluate and plot the effects.
[13]:
grid_size = 100
x_0 = np.linspace(0.1, 0.9, grid_size)
x_1 = np.linspace(0.1, 0.9, grid_size)
x_0, x_1 = np.meshgrid(x_0, x_1)
new_data = {"x_0": x_0.ravel(), "x_1": x_1.ravel()}
[14]:
spline_grid = pd.DataFrame(patsy.build_design_matrices([design_matrix.design_info], new_data)[0])
df_cate = cate.confint(spline_grid, joint=True, n_rep_boot=2000)
print(df_cate)
2.5 % effect 97.5 %
0 1.333704 2.035264 2.736823
1 1.349638 2.035441 2.721245
2 1.376760 2.042249 2.707738
3 1.412726 2.055171 2.697616
4 1.455091 2.073694 2.692297
... ... ... ...
9995 3.543691 4.251412 4.959132
9996 3.582146 4.332502 5.082858
9997 3.619128 4.416132 5.213135
9998 3.659339 4.502595 5.345852
9999 3.707125 4.592186 5.477247
[10000 rows x 3 columns]
[15]:
import plotly.graph_objects as go
grid_array = np.array(list(zip(x_0.ravel(), x_1.ravel())))
true_effect = treatment_effect(grid_array).reshape(x_0.shape)
effect = np.asarray(df_cate['effect']).reshape(x_0.shape)
lower_bound = np.asarray(df_cate['2.5 %']).reshape(x_0.shape)
upper_bound = np.asarray(df_cate['97.5 %']).reshape(x_0.shape)
fig = go.Figure(data=[
go.Surface(x=x_0,
y=x_1,
z=true_effect),
go.Surface(x=x_0,
y=x_1,
z=upper_bound, showscale=False, opacity=0.4,colorscale='purp'),
go.Surface(x=x_0,
y=x_1,
z=lower_bound, showscale=False, opacity=0.4,colorscale='purp'),
])
fig.update_traces(contours_z=dict(show=True, usecolormap=True,
highlightcolor="limegreen", project_z=True))
fig.update_layout(scene = dict(
xaxis_title='X_0',
yaxis_title='X_1',
zaxis_title='Effect'),
width=700,
margin=dict(r=20, b=10, l=10, t=10))
fig.show()